
题目列表(包括答案和解析)
答案:(1)如图
(2)答:这条船继续前进,没有被浅滩阻碍的危险。
解:作CD⊥直线AB于点D,
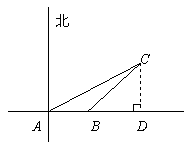 由已知可得∠CAD=30°, ∠CBD=45°,
由已知可得∠CAD=30°, ∠CBD=45°,
AB=100米。
设CD=![]() 米。
米。
在Rt△ACD中
tan∠CAD=![]()
∴AD=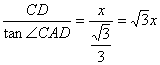
在Rt△CBD中
∵∠CBD=45°, ∴BD=CD=x,
∵AD-BD=AB, ∴![]() 。
。
解得![]()
∴这条船继续前进没有被浅滩阻碍的危险。
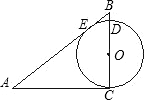 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,以BC上一点O为圆心作⊙O与AB相切于E,与AC相切于C,又⊙O与BC的另一交点为D,则线段BD的长为( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,以BC上一点O为圆心作⊙O与AB相切于E,与AC相切于C,又⊙O与BC的另一交点为D,则线段BD的长为( )| A、1 | ||
B、
| ||
C、
| ||
D、
|
 如图,在Rt△ABC中,∠A=90°,AC=6cm,AB=8cm,现将AB边翻折,使AB边落在BC边上,点A落在点E处,折痕为BD,那tan∠DBE的值为( )
如图,在Rt△ABC中,∠A=90°,AC=6cm,AB=8cm,现将AB边翻折,使AB边落在BC边上,点A落在点E处,折痕为BD,那tan∠DBE的值为( )已知:在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=32,且BD:DC=9:7,则点D到AB边的距离为( )
A.18 B.16 C.14 D.12
【答案】14![]() 。
。
【考点】轴对称-最短路线问题;勾股定理;垂径定理.
【专题】探究型.
【分析】先由MN=20求出⊙O的半径,再连接OA、OB,由勾股定理得出OD、OC的长,作点B关于MN的对称点B′,连接AB′,则AB′即为PA+PB的最小值,B′D=BD=6,过点B′作AC的垂线,交AC的延长线于点E,在Rt△AB′E中利用勾股定理即可求出AB′的值.
【解答】∵MN=20,
∴⊙O的半径=10,
连接OA、OB,
在Rt△OBD中,OB=10,BD=6,
∴OD=![]() =
=![]() =8;
=8;
同理,在Rt△AOC中,OA=10,AC=8,
∴OC=![]() =
=![]() =6,
=6,
∴CD=8+6=14,
作点B关于MN的对称点B′,连接AB′,则AB′即为PA+PB的最小值,B′D=BD=6,过点B′作AC的垂线,交AC的延长线于点E,
在Rt△AB′E中,
∵AE=AC+CE=8+6=14,B′E=CD=14,
∴AB′=![]() =
=![]() =14
=14![]() .
.
故答案为:14![]() .
.
【点评】本题考查的是轴对称-最短路线问题、垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com