练习册

  • 练习册
  • 试题
    我们习惯上把称为切点三角形.在关于两圆外切关系的几何证明题中,运用切点三角形来分析问题,解决问题,可以收到事半功倍的效果,它的应用在两圆外切中尤为重要.性质(4) 切点三角形是直角三角形. 【查看更多】

     

    题目列表(包括答案和解析)

    如图，点D为线段AB上一点，且AD2=BD•AB，我们说点D是线段AB的黄金分割点，为了探求AD与AB的关系，把BD=AB-AD代入得AD2=（AB-AD）•AB，整理得AD2+AB•AD-AB2=0，利用求根公式并舍去负值得AD=数学公式AB≈0.618AB，数学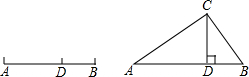上把数学公式称为黄金数．
    （1）如图Rt△ABC中，∠ACB=90°，CD为高，BC=AD
    ①点D是AB的黄金分割点吗？______（填“是”或“不是”）
    ②sinA=______．
    （2）定义：我们把五个元素分别相等的两个不全等三角形称为一对奇异三角形．显然奇异三角形相等的元素只能是三个角和两条边，且任一对对应边不可能相等，这对三角形也不可能是等腰的．
    ①上图中Rt△ADC与Rt△ABC是否是一对奇异三角形______（填“是”或“不是”）
    ②请你构造出一对奇异三角形（只要写出每个三角形的三条边即可）．

    查看答案和解析>>

    小明通过实验发现：将一个矩形可以分割成四个全等的矩形，三个全等的矩形，二个全等的矩形，于是他对含60°的直角三角形进行分割研究，发现可以分割成四个全等的三角形，三个全等的三角形，
    （1）请你在图1，图2依次画出分割线，并简要说明画法；
    （2）小明继续想分割成两个全等的三角形，发现比较困难．你能把这个直角三角形分割成两个全等的小三角形吗？若能，画出分割线；若不能，请说明理由．（注：备用图不够用可以另外画）

    查看答案和解析>>

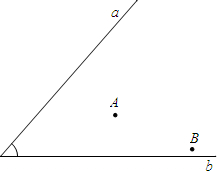    李明准备与朋友合伙经营一个超市，经调查发现他家附近有两个大的居民区A、B，同时又有相交的两条公路a、b（如图），李明想把超市M建在到两居民区的距离相等、且到两条公路距离也相等的位置上，请在答题卷的原图上利用尺规作图作出超市M的位置．（要求：不写已知、求作、做法和结论，保留作图痕迹）

    查看答案和解析>>

    两同心圆中，大圆半径是小圆半径的3倍，把一粒大米抛向两圆，则大米落在圆环内的概率是
     
    ．

    查看答案和解析>>

    14、有一种等腰三角形，经过它的一个顶点的一条直线把这个等腰三角形分成了两个小三角形，这两个小三角形也是等腰三角形，则这种等腰三角形的顶角度数是
    36°或90°或108°
    （至少要写出两种情况）

    查看答案和解析>>


    同步练习册答案