练习册

  • 练习册
  • 试题
    同理可得 【查看更多】

     

    题目列表(包括答案和解析)

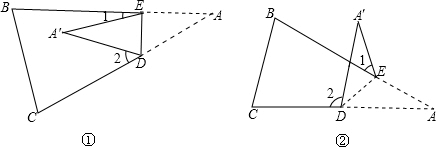
    同学们，在学习了轴对称变换后我们经常会遇到三角形中的“折叠”问题．我们通常会考虑到折叠前与折叠后的图形全等，并利用全等的性质，即对应角相等，对应边相等来研究解决数学中的“折叠”问题．
    （1）如图①，把△ABC纸片沿DE折叠，当点A落在△ABC内部时，我们不仅可以发现AE=A′E，AD=
     
    ，而且我们还可以通过发现∠AED=∠A′ED，∠ADE=∠
     
    ，∠A=∠A′，从而求得∠1+∠2=2∠A．
    （2）如图②，当点A落在△ABC外部时，我们发现∠2=∠DFA+∠
     
    ，∠DFA=∠1+∠
     
    ，那么（1）中的∠1+∠2=2∠A在这里还成立吗？如成立，请说明理由．如不成立，请写出成立的式子并说明理由．
    （3）已知Rt△ABC中，∠C=90°，AC=6，BC=8，将它的一个锐角翻折，使该锐角顶点落在其对边的中点D处，折痕交另一直角边于E，交斜边于F，请你模仿图①，图②，画出相应的示意图并求出△CDE的周长．精英家教网

    查看答案和解析>>

    同时掷两个质地均匀的骰子，观察向上的一面的点数．
    （1）用表格或树状图表示所有可能出现的结果，并求两个骰子点数之和为7的概率；
    （2）小王通过反复试验后得出猜想：两个骰子点数之和为6的概率与两个骰子点数之和为8的概率相等．你认为小王的猜想是否正确？说明理由．

    查看答案和解析>>

    同学们，你会求数轴上两点间的距离吗？
    例如：数轴上，3和5两数在数轴上所对的两点之间的距离可理解为|3-5|=2或理解为5-3=2，5与-2两数在数轴上所对的两点之间的距离可理解为|（-5）-2|=7或|5-（-2）|=7．
    试探索：
    （1）求7与-7两数在数轴上所对的两点之间的距离=
    14
    14
    ．
    （2）找出所有符合条件的整数x，使得|x+3|+|x-1|=4这样的整数是
    ±1、0、-2、-3
    ±1、0、-2、-3
    ．
    （3）由以上探索猜想对于任何有理数x，|x-3|+|x+6|是否有最小值？如果有，写出最小值，如果没有，说明理由．

    查看答案和解析>>

    同学们都知道，|3-（-1）|表示3与-1之差的绝对值，实际上也可理解为3与-1两数在数轴上所对的两点之间的距离．试探索：
    （1）求|3-（-1）|=
    4
    4
    ．
    （2）找出所有符合条件的整数x，使得|x-3|+|x-（-1）|=4，这样的整数是
    -1，0，1，2，3
    -1，0，1，2，3
    ．

    查看答案和解析>>

    同学们都知道，|5-（-2）|表示5与-2之差的绝对值，实际上也可以理解5与-2两数轴上所对的两点之间的距离，试探索：
    （1）求|5-（-2）|=
    7
    7
    ．
    （2）找出所有符合条件的整数x，使得|x+5|+|x-2|=7这样的整数是
    -5，-4，-3，-2，-1，0，1，2
    -5，-4，-3，-2，-1，0，1，2
    ．

    查看答案和解析>>


    同步练习册答案