练习册

  • 练习册
  • 试题
    已知双曲线C的中心在原点.抛物线的焦点是双曲线C的一个焦点.且双曲线过点(1, ). (1)求双曲线的方程; 【查看更多】

     

    题目列表(包括答案和解析)

    （本小题満分12分） 已知中心在原点的双曲线C的右焦点为（2,0），右顶点为。

    （1） 求双曲线C的方程；

    （2） 若直线l：与双曲线C恒有两个不同的交点A和B，且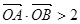（其中O为原点），求k的取值范围。

     

     

    查看答案和解析>>

    （本小题满分12分）. 已知中心在原点的双曲线C的一个焦点是一条渐近线的方程是

      （1）求双曲线C的方程；

      （2）若以为斜率的直线与双曲线C相交于两个不同的点M，N，且线段MN的垂直平分线与两坐标轴围成的三角形的面积为，求的取值范围.

     

     

    查看答案和解析>>

    （本小题满分12分＞
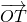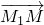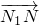    设平面直角坐标中，O为原点，N为动点，|数学公式|=6，数学公式=数学公式•数学公式．过点M作MM1丄y轴于M1，过N作NN1⊥x轴于点N1，数学公式=数学公式+数学公式，记点T的轨迹为曲线C．
    （I）求曲线C的方程：
    （H）已知直线L与双曲线C：5x2-y2=36的右支相交于P、Q两点（其中点P在第-象限）．线段OP交轨迹C于A，若数学公式=3数学公式，S△PAQ=-26tan∠PAQ求直线L的方程．

    查看答案和解析>>

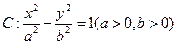    （本小题满分12分）双曲线的离心率为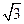，右准线为。
    （Ⅰ）求双曲线C的方程；
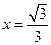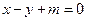    （Ⅱ）已知直线与双曲线C交于不同的两点A，B，且线段AB的中点在圆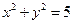上，求m的值.  

    查看答案和解析>>

    (本小题满分12分）

    设平面直角坐标中,O为原点，N为动点，过点M作轴于M1,过N作丄x轴于点N1,,记点R的轨迹为曲线C。 
    (I)求曲线C的方程；

    (II )已知直线L与双曲线C1:的右支相交于P、Q两点（其中点P在第一象限),线段OP交轨迹C于A,若，，求直线L的方程

     

    查看答案和解析>>

    一、选择题（60分）

    BCCA    BDAB    BAAA

    二、填空题（16分）

    13、

    14、0

    15、1

    16、　

    三、解答题（74分）

    17、解（1）,

         ∴递增区间为----------------------6分

      （2）

        而，

          故    --------------- 12分

    18、解：（1）3个旅游团选择3条不同线路的概率为：P1=…………3分

           （2）恰有两条线路没有被选择的概率为：P2=……6分

           （3）设选择甲线路旅游团数为ξ，则ξ=0，1，2，3

           P（ξ=0）=       P（ξ=1）=    

           P（ξ=2）=      P（ξ=3）=

    ξ

    0

    1

    2

    3

                            

          ∴ξ的分布列为：

          

     

     

          ∴期望Eξ=0×+1×+2×+3×=………………12分

    19、

    （1）过O作OF⊥BC于F，连接O1F，

    ∵OO1⊥面AC，∴BC⊥O1F，

    ∴∠O1FO是二面角O1－BC－D的平面角，

    ∵OB=2，∠OBF=60°，∴OF=.

    在Rt△O1OF在，tan∠O1FO=

    ∴∠O1FO=60° 即二面角O1―BC―D为60°

    （2）在△O1AC中，OE是△O1AC的中位线，∴OE∥O1C

    ∴OE∥O1BC，∵BC⊥面O1OF，∴面O1BC⊥面O1OF，交线O1F.

       过O作OH⊥O1F于H，则OH是点O到面O1BC的距离，

    解法二：（1）∵OO1⊥平面AC，

    ∴OO1⊥OA，OO1⊥OB，又OA⊥OB，

    建立如图所示的空间直角坐标系（如图）

    ∵底面ABCD是边长为4，∠DAB=60°的菱形，

    ∴OA=2，OB=2，

    则A（2，0，0），B（0，2，0），C（－2，0，0），O1（0，0，3）

    设平面O1BC的法向量为=（x，y，z），

    则⊥，⊥，

    ∴，则z=2，则x=－，y=3，

    ∴=（－，3，2），而平面AC的法向量=（0，0，3）

    ∴cos<，>=，

    设O1－BC－D的平面角为α， ∴cosα=∴α=60°.

    故二面角O1－BC－D为60°.                

    （2）设点E到平面O1BC的距离为d，

     ∵E是O1A的中点，∴=（－，0，），

    则d=∴点E到面O1BC的距离等于。

    20、解：（1）点都在斜率为6的同一条直线上，

    ，即，

    于是数列是等差数列，故．………………3分

    ，，又与共线，

         …………4分

              

                   ．    ………6分

    当n＝1时，上式也成立．

    所以an．  ……………7分

    （2）把代入上式，

    得

    *   12＜a≤15，，

    *   当n=4时，取最小值，* 最小值为a4=18－2a．   …………12分

    21、解: (1) 由题意设双曲线方程为,把(1,)代入得（*）

    又的焦点是（，0），故双曲线的（2分）与（*）

    联立，消去可得，.

    ∴ ，（不合题意舍去）………（3分）

    于是，∴ 双曲线方程为………（4分）

    (2) 由消去得（*），当

    即（）时，与C有两个交点A、B    ………（5分）

    ① 设A（，），B（，），因，故………（6分）

    即，由（*）知，，代入可得

    ………（7分）

     化简得

    ∴ ，检验符合条件，故当时，………（8分）

    ② 若存在实数满足条件，则必须………（10分）

     由（2）、（3）得………（4）

    把代入（4）得                      ………（11分）

    这与（1）的矛盾，故不存在实数满足条件.          ………（12分）

    22、解:（1）由已知： = ………………………2分

       依题意得：≥0对x∈[1，+∞恒成立………………4分

       ∴ax－1≥0对x∈[1，+∞恒成立    ∴a－1≥0即：a≥1……5分

      （2）∵a=1   ∴由（1）知：f（x）=在[1，+∞上为增函数，

         ∴n≥2时：f（）=  

       即：…7分  

           ∴……………………9分

    设g（x）=lnx－x  x∈[1，+∞， 则对恒成立，

    ∴g′（x）在[1+∞为减函数…………12分

    ∴n≥2时：g（）=ln－<g（1）=－1<0  即：ln<=1+（n≥2）

    ∴

    综上所证：（n∈N*且≥2）成立. ……14分

     

     


    同步练习册答案