
题目列表(包括答案和解析)
如图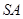 ⊥平面
⊥平面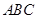 ,
,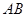 ⊥
⊥ ,过
,过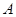 做
做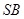
的垂线,垂足为 ,过
,过 做
做 的垂线,垂足为
的垂线,垂足为
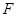 ,求证
,求证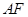 ⊥
⊥ 。以下是证明过程:
。以下是证明过程:
要证
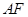 ⊥
⊥
只需证  ⊥平面
⊥平面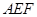
只需证 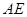 ⊥
⊥ (因为
(因为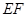 ⊥
⊥ )
)
只需证 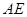 ⊥平面
⊥平面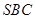
只需证 ① (因为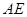 ⊥
⊥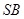 )
)
只需证  ⊥平面
⊥平面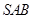
只需证 ② (因为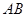 ⊥
⊥ )
)
由只需证 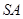 ⊥平面
⊥平面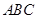 可知上式成立
可知上式成立
所以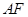 ⊥
⊥
把证明过程补充完整① ②
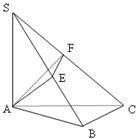
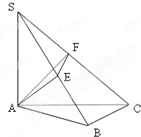 如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程:
如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程: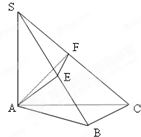 如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程:
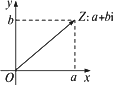
如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程:如下图,设复平面内的点Z表示复数z=a+bi,连结![]() ,显然向量
,显然向量![]() 是由点Z________确定的;反过来,点Z(相对于原点来说)也可以由向量
是由点Z________确定的;反过来,点Z(相对于原点来说)也可以由向量![]() 唯一确定.因此,复数集C与复平面内的向量所成的集合也是一一对应的(实数0与零向量对应),即
唯一确定.因此,复数集C与复平面内的向量所成的集合也是一一对应的(实数0与零向量对应),即
![]()
这是复数的另一种几何意义.
为方便起见,我们常把复数z=a+bi说成点Z或说成向量![]() ,并且规定,相等的向量表示________复数.
,并且规定,相等的向量表示________复数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com