
题目列表(包括答案和解析)
对![]() ,不等式
,不等式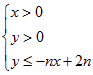 所表示的平面区域为
所表示的平面区域为![]() ,把
,把![]() 内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:
内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:![]()
(1)求![]() ,
,![]() ;
;
(2)数列![]() 满足
满足![]() ,且
,且![]() 时
时![]() .证明当
.证明当![]() 时,
时,
![]() ;
;
(3)在(2)的条件下,试比较![]() 与4的大小关系.
与4的大小关系.
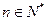 ,不等式
,不等式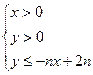 所表示的平面区域为
所表示的平面区域为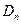 ,把
,把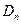 内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:
内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列: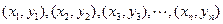
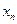 ,
,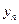 ;
;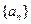 满足
满足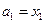 ,且
,且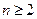 时
时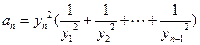 .证明当
.证明当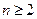 时,
时,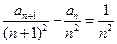 ;
;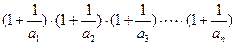 与4的大小关系.
与4的大小关系.
|
| 1 |
| 2y1 |
| 1 |
| 2y2 |
| 1 |
| 2y3 |
| 1 |
| 2yn |
| y | 2 _ |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
|
| y | 2 n |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| an+1 |
| (n+1) |
| an |
| n2 |
| 1 |
| n2 |
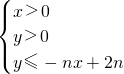 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).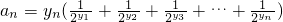 ,求数列{an}的前n项和Sn;
,求数列{an}的前n项和Sn;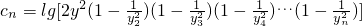 ,且数列{cn}的前n项和Tn,求T99.
,且数列{cn}的前n项和Tn,求T99.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com