
题目列表(包括答案和解析)
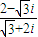 对应的向量为
对应的向量为 ,与复数1+
,与复数1+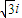 对应的向量为
对应的向量为 ,则
,则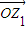 与
与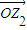 的夹角等于 °.
的夹角等于 °.2-
| ||
|
| OZ1 |
| 3 |
| OZ2 |
| OZ1 |
| OZ2 |
2-
| ||
|
| OZ1 |
| 3 |
| OZ2 |
| OZ1 |
| OZ2 |
复数间的关系
(1)复数相等
①用代数形式描述:
z1=a+bi,z2=c+di(a、b、c、d∈R),
则z1=z2![]() ________.
________.
特殊的,a+bi=0![]() ________.
________.
两个复数不都是实数时,________比较大小.
②用几何形式描述:
z1、z2∈C,z1=z2![]() 对应点Z1、Z2________
对应点Z1、Z2________![]()
![]() 与
与![]() ________.
________.
(2)共轭复数
①定义:若两个复数实部________,虚部________时,这两个复数叫做互为共轭复数,用________表示.
②代数形式:a+bi与________互为共轭复数(a、b∈R),即z=a+bi![]()
![]() =________.
=________.
③几何描述:非零复数z1、z2互为共轭复数![]() 它们的对应点Z1、Z2(或对应向量
它们的对应点Z1、Z2(或对应向量![]() 、
、![]() )关于________对称.
)关于________对称.
④运算性质:
![]() =________;
=________;
![]() =________;
=________;
![]() =________(z2≠0).
=________(z2≠0).
特例:z+![]() =________;z-
=________;z-![]() =________;z·
=________;z·![]() =________;
=________;
z=![]() 是z∈R的________条件;
是z∈R的________条件;
z+![]() =0,且z≠0是z为纯虚数的________条件.
=0,且z≠0是z为纯虚数的________条件.
. | Z |
一、选择题:本小题共8小题,每小题5分,共40分.
题号
1
2
3
4
5
6
7
8
答案
A
B
D
B
D
B
B
C
二、填空题:本小题9―12题必答,13、14、15小题中选答2题,若全答只计前两题得分,共30分.
9. , f(x)<m; 10.90 ; 11.3 ;12.
, f(x)<m; 10.90 ; 11.3 ;12. ;
;
13.垂直; 14. ; 15.
; 15. 。
。
解答提示:
2.解:设等轴双曲线为x2-y2=a2(a>0),
∵焦点到渐近线距离为 ,∴a=
,∴a= 。
。
3.解:∵ , ∴
, ∴
∴ ,∴
,∴ ,∴
,∴ .
.
4.解:只有命题②正确。
5.解:有2男2女和三男一女两种情况,
 =
= 2400种.
2400种.
6.解: ,∴r=3,9时,该项为有理项
,∴r=3,9时,该项为有理项
 ,∴
,∴ 。
。
7.解:由正弦定理得 ,
,
由余弦定理有
 。
。
8.解:
可行域: 的面积为4,圆x2+y2=1的面积为
的面积为4,圆x2+y2=1的面积为 ,
,
由几何概型计算公式得:P= 。
。
10.平均每月注射了疫苗的鸡的数量为 万只。
万只。
11.解: ,
, =3。
=3。
12.解:∵ ,
,
∴ ,
,
又 ,
,
∴ ,夹角等于
,夹角等于 。
。
13.解:垂直。两直线分别过点 和
和 ,前两点和后两点连线显然垂直。
,前两点和后两点连线显然垂直。
法二:两直线化为普通方程是
其斜率乘积 ,故两直线垂直。
,故两直线垂直。
14.解:
 ,应有
,应有
15.解:由圆的相交弦定理知 ,
,
∴ ,
,
由圆的切割线定理知 ,
,
∴ 。
。
三、解答题:
16.解:(1) ,
……………3分
,
……………3分
f(x)
 。
………6分
。
………6分
(2)由(1)知

 , …… 9分
, …… 9分
 的图像向右平移
的图像向右平移 个单位,得到
个单位,得到 的图像,
的图像,
其图像关于原点对称, …………… 11分
故m= 。
……………12分
。
……………12分
17.解:(1) ,
,
又 , ………………………………………………2分
, ………………………………………………2分
又 的等比中项为2,
的等比中项为2, ,
,
而 , ………………………………4分
, ………………………………4分
 , ……………………………6分
, ……………………………6分
(2) ,
,  ,
,
 为首项,-1为公差的等差数列。
………………………9分
为首项,-1为公差的等差数列。
………………………9分
 ,
,
 ;当
;当 ;当
;当 ,
,
 最大。 …………………………12分
最大。 …………………………12分
18.解:(1)这位挑战者有两种情况能过关:
①第三个对,前两个一对一错,得20+10+0=30分, ……… ………1分
②三个题目均答对,得10+10+20=40分, ……… ………2分
其概率分别为 ,
……… ………3分
,
……… ………3分
 ,
……… ………4分
,
……… ………4分
这位挑战者过关的概率为
 。 ………
………5分
。 ………
………5分
(2)如果三个题目均答错,得0+0+(-10)=-10分,
如果前两个中一对一错,第三个错,得10+0+(-10)=0分; …… ………6分
前两个错,第三个对,得0+0+20=20分;
如果前两个对,第三个错,得10+10+(-10)=10分; ……… ………7分
故 的可能取值为:-10,0,10,20,30,40.
………….8分
的可能取值为:-10,0,10,20,30,40.
………….8分
 ,
………
………9分
,
………
………9分
 ………………10分
………………10分
 ……… ………11分
……… ………11分
 ……… ………12分
……… ………12分
又由(1), ,
, 
∴ 的概率分布为
的概率分布为

-10
0
10
20
30
40







………………13分
根据 的概率分布,可得
的概率分布,可得 的期望,
的期望,

………14分
19.解:(1) ,∴
,∴ , ∴
, ∴
∵直线l: 与圆x2+y2=b2相切,
与圆x2+y2=b2相切,
∴ =b,∴b=
=b,∴b= ,b2=2, …….3分
,b2=2, …….3分
∴a2=3. ∴椭圆C1的方程是 …………. 4分
…………. 4分
(2)∵|MP|=|MF2|,
∴动点M到定直线l1:x=-1的距离等于它的定点F2(1,0)的距离. …5分
∴动点M的轨迹是以l1为准线,F2为焦点的抛物线, ………….6分
∴ ,p=2 ,
………….7分
,p=2 ,
………….7分
∴点M的轨迹C2的方程为 。
.………….8分
。
.………….8分
(3)由(1)知A(1,2), ,y2≠2,①
,y2≠2,①
则 ,
………….10分
,
………….10分
又因为 ,
,  ,
,
整理得 ,
………….12分
,
………….12分
则此方程有解,
∴ 解得
解得 或
或 ,
………….13分
,
………….13分
又检验条件①:∵y2=2时y0=-6,不符合题意。
∴点C的纵坐标y0的取值范围是 ………….14分
………….14分
20.解法一:(向量法):
 过点
过点 作
作
∵ ⊥平面
⊥平面
∴ ⊥平面
⊥平面
又在 中,
中,
∴
如图,以 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系 .
………….1分
.
………….1分
又在 中,
中, ,
,

∴
又在 中,
中,
∴
则 ………….3分
………….3分
(1)证明:∵
∴
∴
∴
又
∴ ⊥平面
⊥平面 ………….6分
………….6分
又在 中,
中, 、
、 分别是
分别是 、
、 上的动点,
上的动点,
且
∴不论 为何值,都有
为何值,都有
∴ ⊥平面
⊥平面
又 平面
平面
不论 为何值,总有平面
为何值,总有平面 ⊥平面
⊥平面 ………….8分
………….8分
(2)∵ ,∴
,∴ ,
,
∵ ,∴
,∴ ,
,
又∵ ,
, ,
,
设 是平面
是平面 的法向量,则
的法向量,则 .………….10分
.………….10分
又 ,
, ,∵
,∵ =(0,1,0),
=(0,1,0),
∴
令 得
得
∴ ,
………….12分
,
………….12分
∵  是平面
是平面 的法向量,平面
的法向量,平面 与平面
与平面 所成的二面角为
所成的二面角为 ,
,
∴
∴ ,
,
∴ 或
或 (不合题意,舍去),
(不合题意,舍去),
故当平面 与平面
与平面 所成的二面角的大小为
所成的二面角的大小为 时
时 .…….14分
.…….14分
(2)解法二:∵ ,∴
,∴  ,
,
设E(a,b,c),则 ,
,
∴a=1+ ,b=0,c=
,b=0,c= , E(1+
, E(1+ ,0,
,0,  ),
),
∴ )。
)。
其余同解法一
(2)解法三:设 是平面
是平面 的法向量,则
的法向量,则 ,
,
∵
∴
∴
又在 中,
中, ,
,
∴
又在 中,
中,
∴
∴
又 ,且
,且
∴
∴
∴
又
∴
∴ ……………10分
……………10分
∴
令 得
得
∴ …………12分
…………12分
其余同解法一
解法四:(传统法):
(1)证明:∵ ⊥平面
⊥平面
∴ ………….1分
………….1分
又在 中,
中,
∴ ………….2分
………….2分
又
∴ ⊥平面
⊥平面 ………….3分
………….3分
又在 中,
中, 、
、 分别是
分别是 、
、 上的动点,
上的动点,
且
∴ ………….4分
………….4分
∴ ⊥平面
⊥平面 ………….5分
………….5分
又 平面
平面
∴不论 为何值,总有平面
为何值,总有平面 ⊥平面
⊥平面 .
………….6分
.
………….6分
(2)解:作BQ∥CD,则BQ⊥平面 ,
,
∴BQ⊥BC,BQ⊥BE,
又BQ与CD、EF共面,∴平面 与∩平面
与∩平面 =BQ,
=BQ,
∴∠CBE平面 与平面
与平面 所成的二面角的平面角,为
所成的二面角的平面角,为 ,∴
,∴
 ∴
∴ ① ………….9分
① ………….9分
又
∴
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com