
题目列表(包括答案和解析)
(本题12分) 如图,在平行四边形ABCD中,AB在x轴上,D点y轴上,![]() ,
,![]() ,B点坐标为(4,0).点
,B点坐标为(4,0).点![]() 是边
是边![]() 上一点,且
上一点,且![]() .点
.点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,以1厘米/秒的速度分别沿
同时出发,以1厘米/秒的速度分别沿![]() 、
、![]() 向点
向点![]() 运动(当点F运动到点B时,点E随之停止运动),EM、CD的延长线交于点P,FP交AD于点Q.⊙E半径为
运动(当点F运动到点B时,点E随之停止运动),EM、CD的延长线交于点P,FP交AD于点Q.⊙E半径为![]() ,设运动时间为
,设运动时间为![]() 秒。
秒。
(1)求直线BC的解析式。
(2)当![]() 为何值时,
为何值时,![]() ?
?
(3)在(2)问条件下,⊙E与直线PF是否相切;如果相切,加以证明,并求出切点的坐标。如果不相切,说明理由。
(本题12分)在梯形ABCD中,AB∥CD,∠BCD=90,且AB=1,BC=2,tan∠ADC=2;对角线相交于O点,等腰直角三角板的直角顶点落在梯形的顶点C上,使三角板绕点C旋转。
(1)当三角板旋转到图1的位置时,猜想DE与BF的数量关系,并加以证明。
(2)在(1)问条件下,若BE:CE=1:2,∠BEC=135°,求sin∠BFE的值。
 (3)当三角板的一边CF与梯形对角线AC重合时,作DH⊥PE于H,如图2,若OF=
(3)当三角板的一边CF与梯形对角线AC重合时,作DH⊥PE于H,如图2,若OF=![]() 时,求PE及DH的长。
时,求PE及DH的长。
(本题12分)某商场购进一批单价为5元的日用商品.如果以单价7元销售,每天可售出160件.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量每天就相应减少20件.设这种商品的销售单价为x元,商品每天销售这种商品所获得的利润为y元.
(1)给定x的一些值,请计算y的一些值.
| x | … | 7 | 8 | 9 | 10 | 11 | … |
| y | … |
|
|
|
|
| … |
(2)求y与x之间的函数关系式,并探索:当商品的销售单价定为多少元时,该商店销售这种商品获得的利润最大?这时每天销售的商品是多少件?
(本题12分)如图二次函数![]() 的图象经过
的图象经过![]() 和
和![]() 两点,
两点,
且交![]() 轴于点
轴于点![]() .
.

(1)试确定![]() 、
、![]() 的值;
的值;
(2)过点![]() 作
作![]() 轴交抛物线于点D,点
轴交抛物线于点D,点 为此抛物线的顶点,试确定
为此抛物线的顶点,试确定 的形状.
的形状.
(本题12分)如图,已知点A(-4,2)、B(n,-4)是一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求此反比例函数的解析式和点B的坐标;
(2)根据图象写出使一次函数的值小于反比例函数值的x的取值范围.
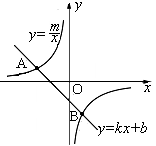
一、选择题(本题共10小题,每小题4分,共40分)
题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
C
A
A
D
B
A
C
B
二、填空题(本题共6小题,每小题5分,共30分)
11. 12.
12. 13.
13.
14. 15.
15. 16.
16.
三、解答题(本题有8小题,共80分)
17.(本题8分)
(1)原式
(2)解: 得:
得: ,
, ,
,
把 代入①得:
代入①得: ,
,
18.(本题8分)
(1)证明: ,
, ,
,
在 和
和 中
中


(2)答案不惟一,如: ,
, ,
, 等.
等.
19.(本题8分)
解:(1)方法一:列表得
A
B
C
D
 A
A
(A,B)
(A,C)
(A,D)
B
(B,A)
(B,C)
(B,D)
C
(C,A)
(C,B)
(C,D)
D
(D,A)
(D,B)
(D,C)
方法二:画树状图


(2)获奖励的概率: .
.
20.(本题8分)
(1)


(2) ,
, ,
, .
.
21.(本题10分)
解:(1)
 是
是 的切线,
的切线,
 ,
,
 ,
, .
.
(2) ,
, ,
, .
.
(3) ,
, ,
, ,
, ,
,
 ,
, .
.
22.(本题12分)
解:(1) ;40;
;40;
(2)人均进球数 .
.
(3)设参加训练前的人均进球数为 个,由题意得:
个,由题意得:
 ,解得:
,解得: .
.
答:参加训练前的人均进球数为4个.
23.(本题12分)
(1)


(2)由题意得: ,
,
 ,
, ,
, (m).
(m).
(3) ,
, ,
,
设 长为
长为 ,则
,则 ,解得:
,解得: (m),即
(m),即 (m).
(m).
同理 ,解得
,解得 (m),
(m), .
.
24.(本题14分)
解:(1)直线 的解析式为:
的解析式为: .
.
(2)方法一, ,
, ,
, ,
,
 ,
, ,
,
 是等边三角形,
是等边三角形, ,
,
 ,
, .
.
方法二,如图1,过 分别作
分别作 轴于
轴于 ,
, 轴于
轴于 ,
,
 可求得
可求得 ,
,
 ,
,

 ,
,
当点 与点
与点 重合时,
重合时,
 ,
,
 .
.
 ,
,

 .
.
(3)①当 时,见图2.
时,见图2.
设 交
交 于点
于点 ,
,
重叠部分为直角梯形 ,
,
作 于
于 .
.
 ,
, ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
 随
随 的增大而增大,
的增大而增大,
 当
当 时,
时, .
.
②当 时,见图3.
时,见图3.
设 交
交 于点
于点 ,
,
交 于点
于点 ,
, 交
交 于点
于点 ,
,
重叠部分为五边形 .
.
方法一,作 于
于 ,
, ,
,
 ,
,
 ,
,
 .
.
方法二,由题意可得 ,
, ,
, ,
, ,
,
再计算
 ,
,

 .
.

 ,
, 当
当 时,
时, 有最大值,
有最大值, .
.
③当 时,
时, ,即
,即 与
与 重合,
重合,
设 交
交 于点
于点 ,
, 交
交 于点
于点 ,重叠部
,重叠部
分为等腰梯形 ,见图4.
,见图4.
 ,
,
综上所述:当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时, .
.
 ,
,
 的最大值是
的最大值是 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com