
题目列表(包括答案和解析)
 ,
, ,
, 为常数,离心率为
为常数,离心率为 的双曲线
的双曲线 :
: 上的动点
上的动点 到两焦点的距离之和的最小值为
到两焦点的距离之和的最小值为 ,抛物线
,抛物线 :
:
 的焦点与双曲线
的焦点与双曲线 的一顶点重合。(Ⅰ)求抛物线
的一顶点重合。(Ⅰ)求抛物线 的方程;(Ⅱ)过直线
的方程;(Ⅱ)过直线 :
: (
( 为负常数)上任意一点
为负常数)上任意一点 向抛物线
向抛物线 引两条切线,切点分别为
引两条切线,切点分别为 、
、 ,坐标原点
,坐标原点 恒在以
恒在以 为直径的圆内,求实数
为直径的圆内,求实数 的取值范围。
的取值范围。
【解析】第一问中利用由已知易得双曲线焦距为 ,离心率为
,离心率为 ,则长轴长为2,故双曲线的上顶点为
,则长轴长为2,故双曲线的上顶点为 ,所以抛物线
,所以抛物线 的方程
的方程
第二问中, 为
为 ,
, ,
, ,
,
故直线 的方程为
的方程为 ,即
,即 ,
,
所以 ,同理可得:
,同理可得:
借助于根与系数的关系得到即 ,
, 是方程
是方程 的两个不同的根,所以
的两个不同的根,所以
由已知易得 ,即
,即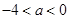
解:(Ⅰ)由已知易得双曲线焦距为 ,离心率为
,离心率为 ,则长轴长为2,故双曲线的上顶点为
,则长轴长为2,故双曲线的上顶点为 ,所以抛物线
,所以抛物线 的方程
的方程
(Ⅱ)设 为
为 ,
, ,
, ,
,
故直线 的方程为
的方程为 ,即
,即 ,
,
所以 ,同理可得:
,同理可得: ,
,
即 ,
, 是方程
是方程 的两个不同的根,所以
的两个不同的根,所以
由已知易得 ,即
,即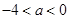
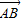 =(-3,4),则
=(-3,4),则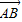 按向量
按向量 =(-2,1)平移后的坐标仍是(-3,4);
=(-2,1)平移后的坐标仍是(-3,4);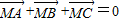 ;
; .
.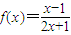 的对称中心是
的对称中心是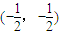 ;
;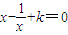 在x∈(0,1)没有实数根,则k的取值范围是k≥2;
在x∈(0,1)没有实数根,则k的取值范围是k≥2;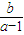 的取值范围为
的取值范围为 ;
;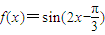 的图象向右平移ϕ(ϕ>0)个单位后变为偶函数,则ϕ的最小值是
的图象向右平移ϕ(ϕ>0)个单位后变为偶函数,则ϕ的最小值是 ;
;| x-1 |
| 2x+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
| b |
| a-1 |
| 1 |
| 3 |
| 2 |
| 3 |
| π |
| 3 |
| 5π |
| 12 |
| x-1 |
| 2x+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
| b |
| a-1 |
| 1 |
| 3 |
| 2 |
| 3 |
| π |
| 3 |
| 5π |
| 12 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com