20．(1)证明:在△A BC中. AB＝AC.AD⊥BC． ∴ ∠BAD＝∠DAC． ------------2分∵ AN是△ABC外角∠CAM的平分线.——青夏教育精英家教网—

20．(1)证明:在△A BC中. AB＝AC.AD⊥BC． ∴ ∠BAD＝∠DAC． ------------2分∵ AN是△ABC外角∠CAM的平分线. 【查看更多】

题目列表(包括答案和解析)

(本小题满分10分)在△ABC中，∠ACB＝90°，∠ABC＝30°，将△ABC绕顶点C顺时针旋转，旋转角为(0°＜＜180°)，得到△A₁B₁C．

(1)如图1，当AB∥CB₁时，设A₁B₁与BC相交于点D．证明：△A₁CD是等边三角形；

(2)如图2，连接AA₁、BB₁，设△ACA₁和△BCB₁的面积分别为S₁、S₂．

求证：S₁∶S₂＝1∶3；

(3)如图3，设AC的中点为E，A₁B₁的中点为P，AC＝a，连接EP．当等于多少度时，EP的长度最大，最大值是多少？

(本小题满分10分)在△ABC中，∠ACB＝90°，∠ABC＝30°，将△ABC绕顶点C顺时针旋转，旋转角为

(0°＜

＜180°)，得到△A₁B₁C．

(1)如图1，当AB∥CB₁时，设A₁B₁与BC相交于点D．证明：△A₁CD是等边三角形；
(2)如图2，连接AA₁、BB₁，设△ACA₁和△BCB₁的面积分别为S₁、S₂．
求证：S₁∶S₂＝1∶3；
(3)如图3，设AC的中点为E，A₁B₁的中点为P，AC＝a，连接EP．当

等于多少度时，EP的长度最大，最大值是多少？

(本小题满分10分)在△ABC中，∠ACB＝90°，∠ABC＝30°，将△ABC绕顶点C顺时针旋转，旋转角为(0°＜＜180°)，得到△A₁B₁C．

(1)如图1，当AB∥CB₁时，设A₁B₁与BC相交于点D．证明：△A₁CD是等边三角形；

(2)如图2，连接AA₁、BB₁，设△ACA₁和△BCB₁的面积分别为S₁、S₂．

求证：S₁∶S₂＝1∶3；

(3)如图3，设AC的中点为E，A₁B₁的中点为P，AC＝a，连接EP．当等于多少度时，EP的长度最大，最大值是多少？

(本小题满分10分)在△ABC中，∠ACB＝90°，∠ABC＝30°，将△ABC绕顶点C顺时针旋转，旋转角为

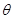(0°＜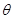

＜180°)，得到△A₁B₁C．

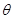等于多少度时，EP的长度最大，最大值是多少？

一节数学课后，老师布置了一道课后练习：

下图，已知在Rt△ABC中，AB＝BC，∠ABC＝90°，BO⊥AC于点O，点P，D分别在AO和BC上，PB＝PD，DE⊥AC于点E．

求证：△BPO≌△PDE．

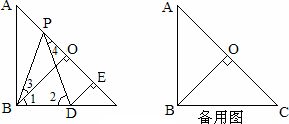
(1)理清思路，完成解答

本题证明的思路可以用下列框图表示：

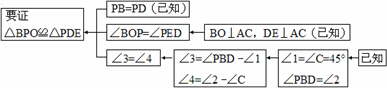
根据上述思路，请你完整地书写本题的证明过程．

(2)特殊位置，证明结论

若BP平分∠ABO，其余条件不变，求证：AP＝CD；

(3)知识迁移，探索新知

若点P是一个动点，当点P运动到OC的中点时，满足题中条件的点D也随之在直线BC上运动到点，请直接写出C与A的数量关系(不必写解答过程)．

同步练习册答案