
题目列表(包括答案和解析)
【答案】![]() π.
π.
【考点】扇形面积的计算;三角形内角和定理.
【分析】根据三角形内角和定理得到∠B+∠C=180°-∠A=130°,利用半径相等得到OB=OD,OC=OE,则∠B=∠ODB,∠C=∠OEC,再根据三角形内角和定理得到∠BOD=180°-2∠B,∠COE=180°-2∠C,则∠BOD+∠COE=360°-2(∠B+∠C)=360°-2×130°=100°,图中阴影部分由两个扇形组成,它们的圆心角的和为100°,半径为3,然后根据扇形的面积公式计算即可.
【解答】∵∠A=50°,
∴∠B+∠C=180°-∠A=130°,
而OB=OD,OC=OE,
∴∠B=∠ODB,∠C=∠OEC,
∴∠BOD=180°-2∠B,∠COE=180°-2∠C,
∴∠BOD+∠COE=360°-2(∠B+∠C)
=360°-2×130°=100°,
而OB=![]() BC=3,
BC=3,
∴S阴影部分=![]() =
=![]() π.
π.
故答案为![]() π.
π.
【点评】本题考查了扇形面积的计算:扇形的面积=![]() (n为圆心角的度数,R为半径).也考查了三角形内角和定理.
(n为圆心角的度数,R为半径).也考查了三角形内角和定理.
如图,点A,B,C,D都在⊙O上, 的度数等于84°,则∠ABD+∠ACO=_____度.
的度数等于84°,则∠ABD+∠ACO=_____度.
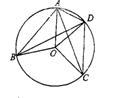
如图,已知∠ABO=20°,∠ACO=25°,∠A=55°,则![]() ∠BOC的度数是___.
∠BOC的度数是___.
 |
如图,点A,B,C,D都在⊙O上,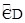 的度数等于84°,则∠ABD+∠ACO=_____度.
的度数等于84°,则∠ABD+∠ACO=_____度.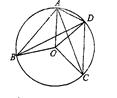
 如图,已知双曲线y=
如图,已知双曲线y=| k |
| x |
| 9 |
| 2 |
| 9 |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com