
题目列表(包括答案和解析)
在△ABC中,角A、B、C的对边分别为a、b、c,向量 =(sinA,b+c),
=(sinA,b+c), =(a-c,sinC-sinB),满足
=(a-c,sinC-sinB),满足 =
=
(Ⅰ)求角B的大小;
(Ⅱ)设 =(sin(C+
=(sin(C+ ),
), ),
),  =(2k,cos2A) (k>1),
=(2k,cos2A) (k>1),  有最大值为3,求k的值.
有最大值为3,求k的值.
【解析】本试题主要考查了向量的数量积和三角函数,以及解三角形的综合运用
第一问中由条件|p +q |=| p -q |,两边平方得p·q=0,又
p=(sinA,b+c),q=(a-c,sinC-sinB),代入得(a-c)sinA+(b+c)(sinC-sinB)=0,
根据正弦定理,可化为a(a-c)+(b+c)(c-b)=0,
即 ,又由余弦定理
,又由余弦定理 =2acosB,所以cosB=
=2acosB,所以cosB= ,B=
,B=
第二问中,m=(sin(C+ ),
), ),n=(2k,cos2A) (k>1),m·n=2ksin(C+
),n=(2k,cos2A) (k>1),m·n=2ksin(C+ )+
)+ cos2A=2ksin(C+B) +
cos2A=2ksin(C+B) + cos2A
cos2A
=2ksinA+ -
- =-
=- +2ksinA+
+2ksinA+ =-
=- +
+ (k>1).
(k>1).
而0<A< ,sinA∈(0,1],故当sin=1时,m·n取最大值为2k-
,sinA∈(0,1],故当sin=1时,m·n取最大值为2k- =3,得k=
=3,得k= .
.
已知正三角形ABC的顶点A(1,1),B(1,3),顶点C在第一象限,若点(x,y)在△ABC内部,则z=-x+y的取值范围是
(A)(1- ,2) (B)(0,2)
(C)(
,2) (B)(0,2)
(C)( -1,2) (D)(0,1+
-1,2) (D)(0,1+ )
)
【解析】 做出三角形的区域如图 ,由图象可知当直线
,由图象可知当直线 经过点B时,截距最大,此时
经过点B时,截距最大,此时 ,当直线经过点C时,直线截距最小.因为
,当直线经过点C时,直线截距最小.因为 轴,所以
轴,所以 ,三角形的边长为2,设
,三角形的边长为2,设 ,则
,则 ,解得
,解得 ,
, ,因为顶点C在第一象限,所以
,因为顶点C在第一象限,所以 ,即
,即 代入直线
代入直线 得
得 ,所以
,所以 的取值范围是
的取值范围是 ,选A.
,选A.
因客流量临时增大,某鞋店拟用一个高为50 cm(即EF=50 cm)的平面镜自制一个竖直摆放的简易鞋镜.根据经验,一般顾客AB的眼睛B到地面的距离x(cm)在区间[140,180]内.设支架FG高为h(0<h<90)cm,AG=100 cm,顾客可视的镜像范围为CD(如图所示),记CD的长度为y(y=GD-GC).
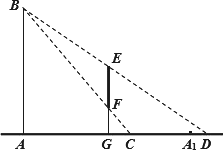
(1)当h=40 cm时,试求y关于x的函数关系式和y的最大值;
(2)当顾客的鞋A在镜中的像A1满足不等关系GC<GA1≤GD(不计鞋长)时,称顾客可在镜中看到自己的鞋,若一般顾客都能在镜中看到自己的鞋,试求h的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com