
题目列表(包括答案和解析)
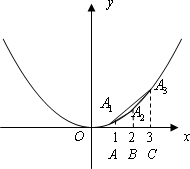
(1)如图,A1,A2,A3是抛物线![]() 图象上的三点,若A1,A2,A3三点的横坐标从左至右依次为1,2,3.求△A1A2A3的面积.
图象上的三点,若A1,A2,A3三点的横坐标从左至右依次为1,2,3.求△A1A2A3的面积.
(2)若将(1)问中的抛物线改为![]() 和y=ax2+bx+c(a>0),其他条件不变,请分别直接写出两种情况下△A1A2A3的面积.
和y=ax2+bx+c(a>0),其他条件不变,请分别直接写出两种情况下△A1A2A3的面积.
(3)现有一抛物线组:![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;……依据变化规律,请你写出抛物线组第n个式子yn的函数解析式;现在x轴上有三点A(1,0),B(2,0),C(3,0).经过A,B,C向x轴作垂线,分别交抛物线组y1,y2,y3,……,yn于A1,B1,C1;A2,B2,C2;A3,B3,C3;……;An,Bn,Cn.记
;……依据变化规律,请你写出抛物线组第n个式子yn的函数解析式;现在x轴上有三点A(1,0),B(2,0),C(3,0).经过A,B,C向x轴作垂线,分别交抛物线组y1,y2,y3,……,yn于A1,B1,C1;A2,B2,C2;A3,B3,C3;……;An,Bn,Cn.记![]() 为S1,
为S1,![]() 为S2,……,
为S2,……,![]() 为Sn,试求S1+S2+S3+……+S10的值.
为Sn,试求S1+S2+S3+……+S10的值.
(4)在(3)问条件下,当n>10时有Sn-10+Sn-9+Sn-8+……+Sn的值不小于![]() ,请探求此条件下正整数n是否存在最大值,若存在,请求出此值;若不存在,请说明理由.
,请探求此条件下正整数n是否存在最大值,若存在,请求出此值;若不存在,请说明理由.
定义:若抛物线的顶点与x轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为:“美丽抛物线”.如图,直线l:y=![]() x+b经过点M(0,
x+b经过点M(0,![]() ),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),……Bn(n,yn)(n为正整数),依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),……An+1(xn+1,0)(n为正整数).若x1=d(0<d<1),当d为()时,这组抛物线中存在美丽抛物线?
),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),……Bn(n,yn)(n为正整数),依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),……An+1(xn+1,0)(n为正整数).若x1=d(0<d<1),当d为()时,这组抛物线中存在美丽抛物线?

A.![]() 或
或![]()
B.![]() 或
或![]()
C.![]() 或
或![]()
D.![]()
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com