
题目列表(包括答案和解析)
如图所示的长方体 中,底面
中,底面 是边长为
是边长为 的正方形,
的正方形, 为
为 与
与 的交点,
的交点, ,
, 是线段
是线段 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求二面角 的大小.
的大小.
【解析】本试题主要考查了线面平行的判定定理和线面垂直的判定定理,以及二面角的求解的运用。中利用 ,又
,又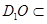 平面
平面 ,
, 平面
平面 ,∴
,∴ 平面
平面 由
由 ,
, ,又
,又 ,∴
,∴ 平面
平面 .
可得证明
.
可得证明
(3)因为∴ 为面
为面 的法向量.∵
的法向量.∵ ,
, ,
,
∴ 为平面
为平面 的法向量.∴利用法向量的夹角公式,
的法向量.∴利用法向量的夹角公式, ,
,
∴ 与
与 的夹角为
的夹角为 ,即二面角
,即二面角 的大小为
的大小为 .
.
方法一:解:(Ⅰ)建立如图所示的空间直角坐标系.连接 ,则点
,则点 、
、 ,
,

∴ ,又点
,又点 ,
, ,∴
,∴
∴ ,且
,且 与
与 不共线,∴
不共线,∴ .
.
又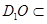 平面
平面 ,
, 平面
平面 ,∴
,∴ 平面
平面 .…………………4分
.…………………4分
(Ⅱ)∵ ,
,
∴ ,
, ,即
,即 ,
, ,
,
又 ,∴
,∴ 平面
平面 . ………8分
. ………8分
(Ⅲ)∵ ,
, ,∴
,∴ 平面
平面 ,
,
∴ 为面
为面 的法向量.∵
的法向量.∵ ,
, ,
,
∴ 为平面
为平面 的法向量.∴
的法向量.∴ ,
,
∴ 与
与 的夹角为
的夹角为 ,即二面角
,即二面角 的大小为
的大小为
在棱长为 的正方体
的正方体 中,
中, 是线段
是线段 的中点,
的中点, .
.
(1) 求证: ^
^ ;
;
(2) 求证: //平面
//平面 ;
;
(3) 求三棱锥 的表面积.
的表面积.

【解析】本试题考查了线线垂直和线面平行的判定定理和表面积公式的运用。第一问中,利用 ,得到结论,第二问中,先判定
,得到结论,第二问中,先判定 为平行四边形,然后
为平行四边形,然后 ,可知结论成立。
,可知结论成立。
第三问中, 是边长为
是边长为 的正三角形,其面积为
的正三角形,其面积为 ,
,
因为 平面
平面 ,所以
,所以 ,
,
所以 是直角三角形,其面积为
是直角三角形,其面积为 ,
,
同理 的面积为
的面积为 ,
,
 面积为
面积为 . 所以三棱锥
. 所以三棱锥 的表面积为
的表面积为 .
.
解: (1)证明:根据正方体的性质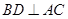 ,
,
因为 ,
,
所以 ,又
,又 ,所以
,所以 ,
, ,
,
所以 ^
^ .
………………4分
.
………………4分
(2)证明:连接 ,因为
,因为 ,
,
所以 为平行四边形,因此
为平行四边形,因此 ,
,
由于 是线段
是线段 的中点,所以
的中点,所以 , …………6分
, …………6分
因为
 面
面 ,
,
 平面
平面 ,所以
,所以 ∥平面
∥平面 . ……………8分
. ……………8分
(3) 是边长为
是边长为 的正三角形,其面积为
的正三角形,其面积为 ,
,
因为 平面
平面 ,所以
,所以 ,
,
所以 是直角三角形,其面积为
是直角三角形,其面积为 ,
,
同理 的面积为
的面积为 ,
……………………10分
,
……………………10分
 面积为
面积为 . 所以三棱锥
. 所以三棱锥 的表面积为
的表面积为

如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
(1) 求证:A1C⊥平面BCDE;
(2) 若M是A1D的中点,求CM与平面A1BE所成角的大小;
(3) 线段BC上是否存在点P,使平面A1DP与平面A1BE垂直?说明理由
【解析】(1)∵ DE∥BC∴
DE∥BC∴ ∴
∴ ∴
∴ ∴
∴ 又∵
又∵ ∴
∴
(2)如图,以C为坐标原点,建立空间直角坐标系C-xyz,

则

设平面 的法向量为
的法向量为 ,则
,则 ,又
,又 ,
, ,所以
,所以 ,令
,令 ,则
,则 ,所以
,所以 ,
,
设CM与平面 所成角为
所成角为 。因为
。因为 ,
,
所以
所以CM与平面 所成角为
所成角为 。
。
如图,在三棱柱 中,
中, 侧面
侧面 ,
, 为棱
为棱 上异于
上异于 的一点,
的一点, ,已知
,已知 ,求:
,求:
(Ⅰ)异面直线 与
与 的距离;
的距离;
(Ⅱ)二面角 的平面角的正切值.
的平面角的正切值.
【解析】第一问中,利用建立空间直角坐标系
解:(I)以B为原点, 、
、 分别为Y,Z轴建立空间直角坐标系.由于,
分别为Y,Z轴建立空间直角坐标系.由于,

在三棱柱 中有
中有
 ,
,
设


又 侧面
侧面 ,故
,故 . 因此
. 因此 是异面直线
是异面直线 的公垂线,则
的公垂线,则 ,故异面直线
,故异面直线 的距离为1.
的距离为1.
(II)由已知有 故二面角
故二面角 的平面角
的平面角 的大小为向量
的大小为向量 与
与 的夹角.
的夹角.

如图,四棱锥P-ABCD中,底面ABCD为菱形,PA 底面ABCD,AC=
底面ABCD,AC= ,PA=2,E是PC上的一点,PE=2EC。
,PA=2,E是PC上的一点,PE=2EC。

(I)
证明PC 平面BED;
平面BED;
(II) 设二面角A-PB-C为90°,求PD与平面PBC所成角的大小
【解析】本试题主要是考查了四棱锥中关于线面垂直的证明以及线面角的求解的运用。
从题中的线面垂直以及边长和特殊的菱形入手得到相应的垂直关系和长度,并加以证明和求解。
解法一:因为底面ABCD为菱形,所以BD AC,又
AC,又




【点评】试题从命题的角度来看,整体上题目与我们平时练习的试题和相似,底面也是特殊的菱形,一个侧面垂直于底面的四棱锥问题,那么创新的地方就是点E的位置的选择是一般的三等分点,这样的解决对于学生来说就是比较有点难度的,因此最好使用空间直角坐标系解决该问题为好。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com