
题目列表(包括答案和解析)
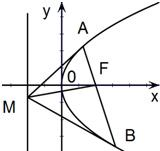 设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A,B两点,且A,B两点坐标分别为(x1,y1)、(x2,y2),y1>0,y2<0,M是抛物线的准线上的一点,O是坐标原点.若直线MA,MF,MB的斜率分别记为:KMA=a,KMF=b,KMB=c,(如图)
设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A,B两点,且A,B两点坐标分别为(x1,y1)、(x2,y2),y1>0,y2<0,M是抛物线的准线上的一点,O是坐标原点.若直线MA,MF,MB的斜率分别记为:KMA=a,KMF=b,KMB=c,(如图)| 1 | 2 |
(08年杨浦区测试)设抛物线![]() 的焦点为
的焦点为![]() ,经过点
,经过点![]() 的直线交抛物线于
的直线交抛物线于![]() 、
、![]() 两点,且
两点,且![]() 、
、![]() 两点坐标分别为
两点坐标分别为![]() ,
,![]() 是抛物线的准线上的一点,
是抛物线的准线上的一点,![]() 是坐标原点.若直线
是坐标原点.若直线![]() 、
、![]() 、
、![]() 的斜率分别记为:
的斜率分别记为:![]() 、
、![]() 、
、![]() ,(如图)
,(如图)
(1)若![]() ,求抛物线的方程.
,求抛物线的方程.
(2)当![]() 时,求
时,求![]() 的值.
的值.
(3)如果取![]() ,
,![]() 时,
时,
(文科考生做)判定![]() 和
和![]() 的值大小关系.并说明理由.
的值大小关系.并说明理由.
(理科考生做)判定![]() 和
和![]() 的值大小关系.并说明理由.
的值大小关系.并说明理由.
通过你对以上问题的研究,请概括出在怎样的更一般的条件下,使得你研究的结果(即![]() 和
和![]() 的值大小关系)不变,并证明你的结论.
的值大小关系)不变,并证明你的结论.
抛物线有光学性质: 由其焦点射出的光线经抛物线折射后,沿平行于抛物线对称轴的方向射出,今有抛物线y2=2px(p>0)![]() 一光源在点M(
一光源在点M(![]() ,4)处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,折射后又射向抛物线上的点Q,再折射后,又沿平行于抛物线的轴的方向射出,途中遇到直线l: 2x-4y-17=0上的点N,再折射后又射回点M(如下图所示)
,4)处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,折射后又射向抛物线上的点Q,再折射后,又沿平行于抛物线的轴的方向射出,途中遇到直线l: 2x-4y-17=0上的点N,再折射后又射回点M(如下图所示)

(1)设P、Q两点坐标分别为(x1,y1)、(x2,y2),证明:y1·y2=-p2;
(2)求抛物线的方程;
(3)试判断在抛物线上是否存在一点,使该点与点M关于PN所在的直线对称?若存在,请求出此点的坐标;若不存在,请说明理由.
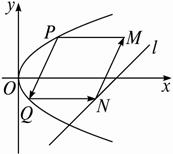
(1)设P、Q两点坐标分别为(x1,y1)、(x2,y2),证明y1·y2=-p2;
(2)求抛物线的方程;
(3)试判断在抛物线上是否存在一点,使该点与点M关于PN所在的直线对称?若存在,请求出此点的坐标;若不存在,请说明理由.
 时,判定|∠AMF-∠BMF|和∠MFO的值大小关系.并说明理由.
时,判定|∠AMF-∠BMF|和∠MFO的值大小关系.并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com