给出以下4个命题，其中所有正确结论的序号是________．

(1)当a为任意实数时，直线(a－1)x－y＋2a＋1＝0恒过定点P，则焦点在y轴上且过点P的抛物线的标准方程是x²＝y．

(2)若直线l₁＋2kx＋(k＋1)y＋1＝0与直线l₂：x－ky＋2＝0垂直，则实数k＝1；

(3)已知数列{a_n}对于任意p，q∈N^*，有a_p＋a_q＝a_p+q，若a₁＝，则a₃₆＝4

(4)对于一切实数x，令[x]为不大于x的最大整数，例如：[3.05]＝3，[]＝1，则函数f(x)＝[x]称为高斯函数或取整函数，若a_n＝f()(n∈N^*)，S_n为数列{a_n}的前n项和，则S₃₀＝145

设F₁、F₂分别为椭圆C：＝1(a＞b＞0)的左、右两个焦点．

(1)若椭圆C上的点A(1，)到F₁、F₂两点的距离之和等于4，写出椭圆C的方程和焦点坐标；

(2)设点K是(1)中所得椭圆上的动点，求线段F₁K的中点的轨迹方程；

(3)已知椭圆具有性质：若M、N是椭圆C上关于原点对称的两个点，点P是椭圆上任意一点，当直线PM、PN的斜率都存在，并记为k_PM、k_PN时，那么k_PM与k_PN之积是与点P位置无关的定值，试写出双曲线＝1具有类似特性的性质并加以证明．

两县城A和B相距20 km，现计划在两县城外以AB为直径的半圆弧上选择一点C建造垃圾处理厂，其对城市的影响度与所选地点到城市的的距离有关，对城A和城B的总影响度为城A与城B的影响度之和，记C点到城A的距离为x km，建在C处的垃圾处理厂对城A和城B的总影响度为y，统计调查表明：垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比，比例系数为4；对城B的影响度与所选地点到城B的距离的平方成反比，比例系数为k，当垃圾处理厂建在的中点时，对城A和城B的总影响度为0.065．

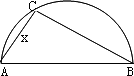
(1)按下列要求建立函数关系式：

(i)设∠CBA＝(rad)，将y表示成的函数；并写出函数的定义域．

(ii)设AC＝x(km)，将y表示成x的函数；并写出函数的定义域．

(2)请你选用(1)中的一个函数关系确定垃圾处理厂的位置，使建在此处的垃圾处理厂对城A和城B的总影响度最小？