
题目列表(包括答案和解析)
下面给出两个抽样问题和三种抽样方法:(1)某小区有800户家庭,其中高收入家庭200户,中等收人家庭480户,低收人家庭120户。为了了解某项购买力的情况,要从中选出一个容量为100的样本。(2)从l0名同学中选出3人参加座谈会。I.简单随机抽样;II.系统抽样;Ⅲ.分层抽样。问题和方法配对正确的是
A.(1)I(2)Ⅱ B.(1)Ⅲ(2)II
C.(1)Ⅱ(2)Ⅲ D.(1)III (2)I
下面给出两个抽样问题和三种抽样方法:(1)某小区有800户家庭,其中高收入家庭200户,中等收人家庭480户,低收人家庭120户。为了了解某项购买力的情况,要从中选出一个容量为100的样本。(2)从l0名同学中选出3人参加座谈会。I.简单随机抽样;II.系统抽样;Ⅲ.分层抽样。问题和方法配对正确的是
A.(1)I(2)Ⅱ B.(1)Ⅲ(2)II
C.(1)Ⅱ(2)Ⅲ D.(1)III (2)I
如图,在四棱锥 中,
中, ⊥底面
⊥底面 ,底面
,底面 为正方形,
为正方形, ,
, ,
, 分别是
分别是 ,
, 的中点.
的中点.
(I)求证: 平面
平面 ;
;
(II)求证: ;
;
(III)设PD=AD=a, 求三棱锥B-EFC的体积.

【解析】第一问利用线面平行的判定定理, ,得到
,得到
第二问中,利用
 ,所以
,所以
又因为 ,
, ,从而得
,从而得
第三问中,借助于等体积法来求解三棱锥B-EFC的体积.
(Ⅰ)证明:
 分别是
分别是 的中点,
的中点, 
 ,
, . …4分
. …4分
(Ⅱ)证明: 四边形
四边形 为正方形,
为正方形, .
.
 ,
,  .
.
 ,
,  ,
,
 .
. ,
, . ………8分
. ………8分
(Ⅲ)解:连接AC,DB相交于O,连接OF, 则OF⊥面ABCD,
∴

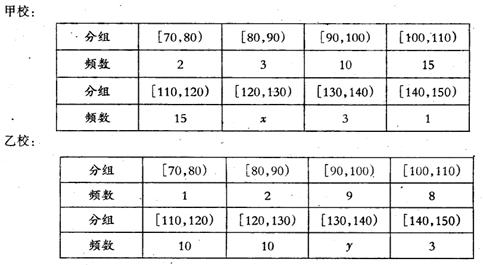
甲乙两个学校高三年级分别有1100人和1000人,为了了解这两个学校全体高三年级学生在该地区二模考试中的数学成绩情况,采用分层抽样方法从两个学校一共抽取了105名学生的数学成绩,并作出了如下的频数分布统汁表,规定考试成绩在[120,150]内为优秀.

(I)试求x,y的值;
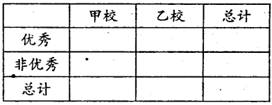
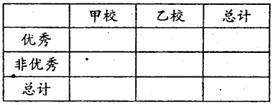
(II)由以上统计数据填写右面2×2列联表,若按是否优秀来判断,是否有97.5%的把握
认为两个学校的数学成绩有差异。
(III)根据抽样结果分别估计甲校和乙校的优秀率,若把频率视为概率,现从乙校学生中任取3人,求优秀学生人数ξ的分布列和数学期望。
附: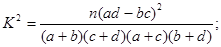
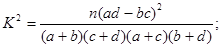
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com