
题目列表(包括答案和解析)
| 10-x |
| 10+x |
| 10-x |
| 10+x |
 x∈A,试判断g(x)的单调性;(不证)
x∈A,试判断g(x)的单调性;(不证) >2x+a-5},若A∩B≠Φ,求实数a的取值范围.
>2x+a-5},若A∩B≠Φ,求实数a的取值范围.给定精确度ε,用二分法求函数f(x)零点近似值的步骤如下:
(1)确定区间[a,b],验证________,给定精确度ε.
(2)求区间(a,b)的中点x1.
(3)计算f(x1).
①若f(x1)=0,则x1就是函数的零点;?
②若f(a)·f(x1)<0,则令________(此时零点x0∈(a,x1));
③若f(x1)·f(b)<0,则令________(此时零点x0∈(x1,b)).
(4)判断是否达到精确度ε:即若________,则得到零点近似值a(或b);否则重复(2)-(4).
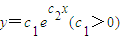 转化为线性回归方程,即两边取对数,令z=lny,得到z=c2x+lnc1.受其启发,可求得函数
转化为线性回归方程,即两边取对数,令z=lny,得到z=c2x+lnc1.受其启发,可求得函数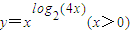 的值域是 .
的值域是 .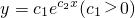 转化为线性回归方程,即两边取对数,令z=lny,得到z=c2x+lnc1.受其启发,可求得函数
转化为线性回归方程,即两边取对数,令z=lny,得到z=c2x+lnc1.受其启发,可求得函数 的值域是________.
的值域是________.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com