
题目列表(包括答案和解析)
设椭圆 的左、右顶点分别为
的左、右顶点分别为 ,点
,点 在椭圆上且异于
在椭圆上且异于 两点,
两点, 为坐标原点.
为坐标原点.
(Ⅰ)若直线 与
与 的斜率之积为
的斜率之积为 ,求椭圆的离心率;
,求椭圆的离心率;
(Ⅱ)若 ,证明直线
,证明直线 的斜率
的斜率
 满足
满足
【解析】(1)解:设点P的坐标为 .由题意,有
.由题意,有 ①
①
由 ,得
,得 ,
,
由 ,可得
,可得 ,代入①并整理得
,代入①并整理得
由于 ,故
,故 .于是
.于是 ,所以椭圆的离心率
,所以椭圆的离心率
(2)证明:(方法一)
依题意,直线OP的方程为 ,设点P的坐标为
,设点P的坐标为 .
.
由条件得 消去
消去 并整理得
并整理得 ②
②
由 ,
, 及
及 ,
,
得 .
.
整理得 .而
.而 ,于是
,于是 ,代入②,
,代入②,
整理得
由 ,故
,故 ,因此
,因此 .
.
所以 .
.
(方法二)
依题意,直线OP的方程为 ,设点P的坐标为
,设点P的坐标为 .
.
由P在椭圆上,有
因为 ,
, ,所以
,所以 ,即
,即 ③
③
由 ,
, ,得
,得 整理得
整理得 .
.
于是 ,代入③,
,代入③,
整理得
解得 ,
,
所以 .
.
已知正数数列{an }中,a1 =2.若关于x的方程 (
( )对任意自然数n都有相等的实根.
)对任意自然数n都有相等的实根.
(1)求a2 ,a3的值;
(2)求证
【解析】(1)中由题意得△ ,即
,即 ,进而可得
,进而可得 ,.
,.
(2)中由于 ,所以
,所以 ,因为
,因为 ,所以数列
,所以数列 是以
是以 为首项,公比为2的等比数列,知数列
为首项,公比为2的等比数列,知数列 是以
是以 为首项,公比为
为首项,公比为 的等比数列,利用裂项求和得到不等式的证明。
的等比数列,利用裂项求和得到不等式的证明。
(1)由题意得△ ,即
,即 ,进而可得
,进而可得
(2)由于 ,所以
,所以 ,因为
,因为 ,所以数列
,所以数列 是以
是以 为首项,公比为2的等比数列,知数列
为首项,公比为2的等比数列,知数列 是以
是以 为首项,公比为
为首项,公比为 的等比数列,于是
的等比数列,于是
 ,
,
所以
某次市教学质量检测,甲、乙、丙三科考试成绩的直方图如图所示(由于人数众多,成绩分布的直方图可视为正态分布),则由图中曲线可得下列说法中正确的一个是
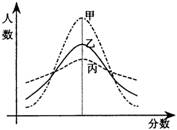
A.甲、乙、丙的总体的平均数不相同
B.乙科总体的标准差及平均数都居中
C.丙科总体的平均数最小
D.甲科总体的标准差最小
在研究某新措施对“非典”的防治效果问题时,得到如下列联表:
|
|
存活数 |
死亡数 |
合计 |
|
新措施 |
132 |
18 |
150 |
|
对照 |
114 |
36 |
150 |
|
合计 |
246 |
54 |
300 |
由表中数据可得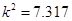 ,故我们由此认为
“新措施对防治非典有效” 的把握为( )
,故我们由此认为
“新措施对防治非典有效” 的把握为( )
A.0
B.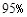 C.
C.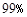 D.
D.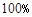
设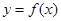 为区间
为区间 上的连续函数,且恒有
上的连续函数,且恒有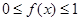 ,可以用随机模拟方法近似计算积分
,可以用随机模拟方法近似计算积分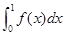 ,先产生两组(每组N个)区间
,先产生两组(每组N个)区间 上的均匀随机数
上的均匀随机数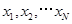 和
和 ,由此得到N个点
,由此得到N个点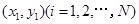 ,再数出其中满足
,再数出其中满足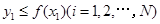 的点数
的点数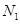 ,那么由随机模拟方案可得积分
,那么由随机模拟方案可得积分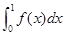 的近似值为 。
的近似值为 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com