练习册

  • 练习册
  • 试题
    38 【查看更多】

     

    题目列表(包括答案和解析)

    如图38所示，质量为M的长平板车放在光滑的倾角为α的斜面上，车上站着一质量为m的人.若要平板车静止在斜面上，车上的人必须 …（    ）

    图3-8

    A.加速向上奔跑

    B.以加速度a=gsinα向下加速奔跑

    C.以加速度a=(1+)gsinα向上加速奔跑

    D.以加速度a=(1+)gsinα向下加速奔跑

       

    查看答案和解析>>

    如图9-38-15所示，边长为L的正方形区域abcd内存在着匀强电场.电量为q、动能为Ek的带电粒子从a点沿ab方向进入电场，不计重力.

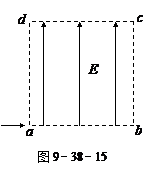
    若粒子从c点离开电场，求电场强度的大小和粒子离开电场时的动能；

    若粒子离开电场时动能为Ek’，则电场强度为多大？

    查看答案和解析>>

    如图9-38-4所示，由A、B两平行金属板构成的电容器放置在真空中，电容为C，原来不带电.电容器的A板接地，并且中心有一个小孔，通过这个小孔向电容器中射入电子，射入的方向垂直于极板，射入的速度为v0，如果电子是间歇发射的，即第一个电子达B板后再发射第二个电子，并且所有到达板的电子都留在B板上.随着电子的射入，两极板间的电势差逐渐增加，直至达到一个稳定值，已知电子的质量为m，电荷量为e电子所受的重力忽略不计，两板的距离为d.

       

    当板上聚集了n个射来的电子时，两板间电场的场强E多大？

    最多能有多少个电子到达B板？

    查看答案和解析>>

    如图9-38-10所示，质量相同的两个带电粒子P、Q以相同速度沿垂直于电场方向射入两平行板间的匀强电场中，P从两板正中央射入，Q从下极板边缘入射入，它们最后打在同一点(重力不计)，则从开始射入到打到上板的过程中（      ）

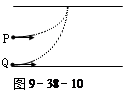
    A.它们的运动时间tQ＞tP

    B.它们所带电量之比qP：qQ=1:2

    C.它们的动能增量之比

    D.它们的电势能减少量之比

    查看答案和解析>>

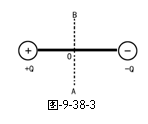
    如图9-38-3所示，一电子沿等量异种电荷的中垂线由 A→O→B匀速飞过，电子重力不计，则电子所受另一个力的大小和方向变化情况是(    )

    A．先变大后变小，方向水平向左

    B．先变大后变小，方向水平向右

    C．先变小后变大，方向水平向左

    D．先变小后变大，方向水平向右

    查看答案和解析>>

    一、二、选择题

    题号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    答案

    C

    B

    C

    A

    D

    CD

    BC

    AC

    ABD

    三、简答题

    10．每小题2分,计8分。

    （1）C；

    （2）；

    （3）m<<M；

    （4）如图所示。

    11．（3）4分，其余每小题2分,计10分。

    （1）保护电源、电表，防止短路；

    （2）作图；

    （3）1．5，     1．0    （3.0不正确）

    （4）30，5

    12A．（每小题4分，计12分）

    （1）CD

    （2）AB

    （3）1.2×10-5Pa；内能增加了1.8×105J

    12B．（每小题4分，计12分）

    （1）①1：3    ②4：1

    （2）CD

    （3）（3）发生；450

    12C．（每小题4分，计12分）

    （1）C

    （2）B

    （3）2

    四、全题共计47分．解答时请写出必要的文字说明、方程式和重要的演算步骤．只写出最后答案的不能得分．有数值计算的题．答案中必须明确写出数值和单位

    13．解：（1）在D点，速度为vD，

    mg = mvD2/R

    ∴v=2m/s

    由A运动到D点，机械能守恒

    mg（h-2R）= mvD2/2

    ∴h=1m

    （2）由A运动到C点，机械能守恒

    mgh=mvC2/2

    在C点，由向心力公式，得

    FN-mg=mvC2/R

    ∴FN=12N

    （3）设撞到斜面上E点离B点的距离为x，飞行时间为t，由位移公式，得

    Rsin530+xcos530   = vDt

    R+Rcos530-xsin530 = gt2/2

    由上面两式，得

    t = s

    评分：（1）（2）各4分，（3）中列式4分，结果4分。

    14．解：（1）粒子进入磁场后做圆周运动的轨道半径为r

    ∴

    （2）O、P连线与x轴之间的夹角为45°，由运动的对称性，粒子经两个四分之一圆弧到达P点，设圆周运动周期为T0，由T0=，得

                   T0=                 ∴T= =

    （3）设两段圆弧的圆心OO的连线与y轴夹角为θ，P点的纵坐标为y，圆心O到y轴之间的距离为x，则由几何关系，得

    y=2r+2rcosθ

    sinθ=

    保证粒子在第一象限内运动，

    x≥r

    当θ=300时，y取最大，

    ym=（2+）

    评分标准：（1）4分（2）4分，（3中各式2分，计8分。

     

     

    15．解：（1）拉力F作用过程中，在时间△t内，磁通量为△Φ，通过电阻R上电量q

    ，

    ，

    ，

     

    （2）撤去F后金属棒滑行过程中动能转化为电能

    ∵           

    由能量守恒定律，得

       

    ∴          

    （3）匀速运动时最大拉力与安培力平衡

        

     由图像面积，可得拉力做功为  

       

    由动能定理，得           

                   

    电阻R上产生的热量（）

                              

    评分标准：（1）各式1分，计4分（2）各式2分，计6分，（3中各式2分，计6分。

     

     

     

     

     

     

     


    同步练习册答案