
题目列表(包括答案和解析)
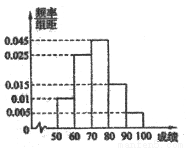
山东省《体育高考方案》于2012年2月份公布,方案要求以学校为单位进行体育测试,某校对高三1班同学按照高考测试项目按百分制进行了预备测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人.
(Ⅰ)请估计一下这组数据的平均数M;
(Ⅱ)现根据初赛成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成一个小组.若选出的两人成绩差大于20,则称这两人为“帮扶组”,试求选出的两人为“帮扶组”的概率.
【解析】本试题主要考查了概率的运算和统计图的运用。
(1)由由频率分布直方图可知:50~60分的频率为0.1, 60~70分的频率为0.25, 70~80分的频率为0.45, 80~90分的频率为0.15, 90~100分的频率为0.05,然后利用平均值公式,可知这组数据的平均数M=55×0.1+65×0.25+75×0.45+85×0.15+95×0.05=73(分)
(2)中利用90~100分数段的人数为2人,频率为0.05;得到总参赛人数为40,然后得到0~60分数段的人数为40×0.1=4人,第五组中有2人,这样可以得到基本事件空间为15种,然后利用其中两人成绩差大于20的选法有:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A4,B1),(A4,B2)共8种,得到概率值
解:(Ⅰ)由频率分布直方图可知:50~60分的频率为0.1, 60~70分的频率为0.25, 70~80分的频率为0.45, 80~90分的频率为0.15, 90~100分的频率为0.05; ……………2分
∴这组数据的平均数M=55×0.1+65×0.25+75×0.45+85×0.15+95×0.05=73(分)…4分
(Ⅱ)∵90~100分数段的人数为2人,频率为0.05;
∴参加测试的总人数为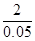 =40人,……………………………………5分
=40人,……………………………………5分
∴50~60分数段的人数为40×0.1=4人, …………………………6分
设第一组50~60分数段的同学为A1,A2,A3,A4;第五组90~100分数段的同学为B1,B2
则从中选出两人的选法有:(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,A4),(A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2),共15种;其中两人成绩差大于20的选法有:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A4,B1),(A4,B2)共8种 …………………………11分
则选出的两人为“帮扶组”的概率为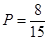
(本题满分12分)
某学校的课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表所示:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
若单科成绩在85分以上(含85分),则该科成绩为优秀.
(1)根据上表完成下面的![]() 列联表(单位:人)
列联表(单位:人)
| 数学成绩优秀 | 数学成绩不优秀 | 总计 | |
| 物理成绩优秀 | |||
| 物理成绩不优秀 | |||
| 总计 | 20 |
(2)根据(1)中表格的数据计算,是否有99%的把握,认为学生的数学成绩与物理成绩之间有关系?
(3)若从这20个人中抽出1人来了解有关情况,求抽到的学生数学成绩与物理成绩至少有一门不优秀的概率.
参考公式:![]()
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
(本题满分12分)某学校课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表所示:
|
序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
数学 成绩 |
95 |
75 |
80 |
94 |
92 |
65 |
67 |
84 |
98 |
71 |
67 |
93 |
64 |
78 |
77 |
90 |
57 |
83 |
72 |
83 |
|
物理 成绩 |
90 |
63 |
72 |
87 |
91 |
71 |
58 |
82 |
93 |
81 |
77 |
82 |
48 |
85 |
69 |
91 |
61 |
84 |
78 |
86 |
若单科成绩85分以上(含85分),则该科成绩为优秀.
(1)根据上表完成下面的2×2列联表(单位:人):
|
|
数学成绩优秀 |
数学成绩不优秀 |
合 计 |
|
物理成绩优秀 |
|
|
|
|
物理成绩不优秀 |
|
|
|
|
合 计 |
|
|
20 |
(2)根据题(1)中表格的数据计算,有多大的把握,认为学生的数学成绩与物理成绩之间有关系?
(3)若从这20个人中抽出1人来了解有关情况,求抽到的学生数学成绩与物理成绩至少有一门不优秀的概率.
参考数据及公式:
①随机变量 ,其中
,其中 为样本容量;
为样本容量;
②独立检验随机变量 的临界值参考表:
的临界值参考表:
|
|
0.010 |
0.005 |
0.001 |
|
|
6.635 |
7.879 |
10.828 |
(本题满分12分)某学校课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表所示:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学 成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理 成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
| | 数学成绩优秀 | 数学成绩不优秀 | 合 计 |
| 物理成绩优秀 | | | |
| 物理成绩不优秀 | | | |
| 合 计 | | | 20 |
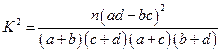 ,其中
,其中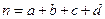 为样本容量;
为样本容量;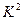 的临界值参考表:
的临界值参考表: | 0.010 | 0.005 | 0.001 |
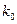 | 6.635 | 7.879 | 10.828 |
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 |
| 物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 |
| 序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学成绩 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理成绩 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 物理成绩优秀 | |||
| 物理成绩不优秀 | 12 | ||
| 合计 | 20 |
| P(K2≥x) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| x | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 .
.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com