
题目列表(包括答案和解析)
(2)二项式系数:二项式展开式第r+1项的二项式系数为_________(r=0,1,2,…,n).?
(3)通项公式:(a+b)n的二项展开式中的_______叫做二项式展开式的通项,用________表示,则有_________.?
(4)指数特征:二项式展开式中a的指数由n_______0,b的指数由0_________,各项a、b的指数之和都等于__________,其中a、b可以为数,也可以是式.
已知 的展开式中第3项的系数与第5项的系数之比为
的展开式中第3项的系数与第5项的系数之比为 .
.
(1)求 的值;(2)求展开式中的常数项.
的值;(2)求展开式中的常数项.
【解析】(1)利用二项展开式的通项公式求出展开式的通项,求出展开式中第3项与第5项的系数列出方程求出n的值.
(2)将求出n的值代入通项,令x的指数为0求出r的值,将r的值代入通项求出展开式的常数项.
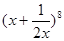 的展开式中
的展开式中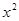 的系数为____________.
的系数为____________.
【解析】二项展开式的通项为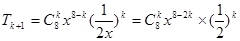 ,令
,令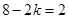 ,解得
,解得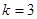 ,所以
,所以 ,所以
,所以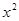 的系数为7.
的系数为7.
若 的展开式中第3项与第7项的二项式系数相等,则该展开式中
的展开式中第3项与第7项的二项式系数相等,则该展开式中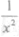 的系数为_________.
的系数为_________.
【解析】因为展开式中的第3项和第7项的二项式系数相同,即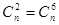 ,所以
,所以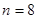 ,所以展开式的通项为
,所以展开式的通项为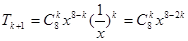 ,令
,令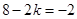 ,解得
,解得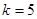 ,所以
,所以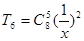 ,所以
,所以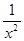 的系数为
的系数为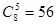 .
.
| B | 1-A |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com