查看答案和解析>>

如右图所示，水平固定的小圆盘A，其带电荷量为Q，电势为零，从圆盘圆心处O静止释放一个质量为m、带电荷量为+q的小球，由于电场的作用，小球竖直上升的高度可达圆盘中心竖直线上的C点，而到圆盘中心竖直线上的b点时，小球速度最大.由此可知Q所形成的电场中，可以确定的物理量是（   ）

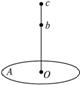
A．b点场强	B．c点场强
C．b点电势	D．c点电势

查看答案和解析>>

查看答案和解析>>

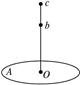
如下图所示，半径为r、质量不计的圆盘面与地面相垂直，圆心处有一个垂直盘面的光滑水平轴O，在盘的最右边缘固定一个质量为m的小球A，在O点的正下方离O点处固定一个质量也为m的小球B，放开盘任其自由转动，问：

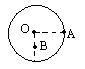
(1)当A球转到最低点时，两小球的重力势能之和减少了多少？

(2)A球转到最低点时的线速度是多少？

查看答案和解析>>

如图所示，半径为r，质量不计的圆盘盘面与地面相垂直，圆心处有一个垂直盘面的光滑水平固定轴O，在盘的最右边缘固定一个质量为m的小球A，在O点的正下方离O点r/2处固定一个质量也为m的小球B．放开盘让其自由转动，问：
（1）当A球转到最低点时，两小球的重力势能之和减少了多少？
（2）A球转到最低点时的线速度是多少？
（3）在转动过程中半径OA向左偏离竖直方向的最大角度是多少？

查看答案和解析>>

一、选择题：

题号

1

2

3

4

5

6

7

8

9

10

答案

C

C

C

B

A

BD

AD

BD

BCD

AD

二、非选择题：

　11、（1）刻度尺  交流 （2）D （3）B（4）GK（学生只要取匀速部分均为正确）（每空2分）

  12、(1)4Hh  (2)(见右下图)

    (3)小于(4)摩擦，转动 (回答任一即可)（每空2分，图4分）

13.解：(1)

得

（2） 　　　　2分

　　　　　1分

　　　　　　　　　　　　　　　　2分

14、 以A、B整体为对象：

    当A、B相互脱离时，N＝0，则以A为研究对象

15、（1）设小物体运动到p点时的速度大小为v，对小物体由a运动到p过程应用动能定理得

                         ①（2分）

                                                      ②（2分）

s=vt                                                                 ③（2分）

联立①②③式，代入数据解得s=0.8m       ④（2分）

（2）设在数字“0”的最高点时管道对小物体的作用力大小为F，取竖直向下为正方向

                                                   ⑤（3分）

联立①⑤式，代入数据解得F＝0.3N            ⑥（3分）

方向竖直向下　　　　　　　　　　　　　　　　　（1分）

16、解：

（1）小球重力所做功为

　　　　　4分

（2）外力F做功 　　　　　　　4分

（3）将小球和框架槽看作一个系统，则系统动能定理：

  　　　　　　　　　　　　　　2分

其中为小球的质量和小球此时的速度，为框架槽的质量和此时的速度．

由运动的分解得： 　　　　　　　　　　　　3分

代入上述方程：：　　　　　　　　　　　　　2分