
题目列表(包括答案和解析)
(本小题满分12分) 甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,
甲先从 道备选题中一次性抽取
道备选题中一次性抽取 道题独立作答,然后由乙回答剩余
道题独立作答,然后由乙回答剩余 题,每人答对其中
题,每人答对其中
题就停止答题,即闯关成功.已知在 道备选题中,甲能答对其中的
道备选题中,甲能答对其中的 道题,乙答对每道题
道题,乙答对每道题
的概率都是 .
.
(Ⅰ)求甲、乙至少有一人闯关成功的概率;
(Ⅱ)设甲答对题目的个数为ξ,求ξ的分布列及数学期望.
(本小题满分12分) 甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,
甲先从 道备选题中一次性抽取
道备选题中一次性抽取 道题独立作答,然后由乙回答剩余
道题独立作答,然后由乙回答剩余 题,每人答对其中
题,每人答对其中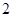
题就停止答题,即闯关成功.已知在 道备选题中,甲能答对其中的
道备选题中,甲能答对其中的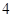 道题,乙答对每道题
道题,乙答对每道题
的概率都是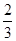 .
.
(Ⅰ)求甲、乙至少有一人闯关成功的概率;
(Ⅱ)设甲答对题目的个数为ξ,求ξ的分布列及数学期望.
本小题满分12分)
甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次.记录如下:
甲:82 81 79 78 95 88 93 84 乙:92 95 80 75 83 80 90 85
(1)画出甲、乙两位学生成绩的茎叶图,指出学生乙成绩的中位数;
(2)现要从中选派一人参加数学竞赛,从平均状况和方差的角度考虑,你认为派哪位学生参加合适?请说明理由;
(3)若将频率视为概率,对学生甲在今后的三次数学竞赛成绩进行预测,记这三次成绩中高于80分的次数为 ,求
,求 的分布列及数学期望
的分布列及数学期望 .
.
(本小题满分12分)
甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次.记录如下:
甲:82 81 79 78 95 88 93 84 乙:92 95 80 75 83 80 90 85
(1)画出甲、乙两位学生成绩的茎叶图,指出学生乙成绩的中位数;
(2)现要从中选派一人参加数学竞赛,从平均状况和方差的角度考虑,你认为派哪位学生参加合适?请说明理由;
(3)若将频率视为概率,对学生甲在今后的三次数学竞赛成绩进行预测,记这三次成绩中高于80分的次数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
( 本小题满分12分)
甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次.记录如下:
甲:82 81 79 78 95 88 93 84 乙:92 95 80 75 83 80 90 85
(I)画出甲、乙两位学生成绩的茎叶图,指出学生乙成绩的中位数;
(II)现要从中选派一人参加数学竞赛,从平均状况和方差的角度考虑,你认为派哪位学生参加合适?请说明理由;
(III)若将频率视为概率,对学生甲在今后的三次数学竞赛成绩进行预测,记这三次成绩中高于80分的次数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
一、选择题 A D B A C B A D A C B B
二、填空题
13. . 14.
. 14. 15.
15.  .16.①②③④
.16.①②③④
三、解答题
17.(1)
 =
=
=
= =
=
= =
= .
.
∴ 的最小正周期
的最小正周期 .
.
(2) ∵
 , ∴
, ∴ .
.
∴当 ,即
,即 =
= 时,
时, 有最大值
有最大值 ;
;
当 ,即
,即 =
= 时,
时, 有最小值-1.
有最小值-1.
18. (1)连结 ,则
,则 是
是 的中点,
的中点,
 在△
在△ 中,
中, ,
,
且
 平面
平面 ,
,
 平面
平面 ,
,
∴ ∥平面
∥平面
(2) 因为 平面
平面 ,
,
 平面
平面 ,
,
 ,
,
又 ⊥
⊥ ,所以,
,所以, ⊥平面
⊥平面 ,
,
∴四边形  是矩形,
是矩形,
且侧面 ⊥平面
⊥平面
取 的中点
的中点



 ,
, ,
,
且 平面
平面 .
.
所以,多面体 的体积
的体积
19.解:(Ⅰ)依题意,甲答对试题数 的概率分布如下:
的概率分布如下:

0
1
2
3





甲答对试题数 的数学期望:
的数学期望:

(Ⅱ)设甲、乙两人考试合格的事件分别为
则 

甲、乙两人考试均不合格的概率为:

∴甲、乙两人至少一个合格的概率为

20.(1) ,
,
∴  ,于是
,于是 ,
,
∴ 为首相和公差均为1的等差数列.
为首相和公差均为1的等差数列.
由  ,
, 得,
得, 
∴ .
.
(2) ,
,
 ,
,
两式相减,得 ,
,
解出
21. 因
而函数 在
在 处取得极值2
处取得极值2
所以 




所以  为所求
为所求


 (2)由(1)知
(2)由(1)知
可知, 的单调增区间是
的单调增区间是
所以,


所以当 时,函数
时,函数 在区间
在区间 上单调递增
上单调递增
(3)由条件知,过 的图形上一点
的图形上一点 的切线
的切线 的斜率
的斜率 为:
为:


令 ,则
,则 ,
,
此时 ,
根据二次函数 的图象性质知:
的图象性质知:
当 时,
时,
当 时,
时,
所以,直线 的斜率
的斜率 的取值范围是
的取值范围是
22. 解:(1)∵点A在圆 ,
,

由椭圆的定义知:|AF1|+|AF2|=2a,

(2)∵函数
∴
点F1(-1,0),F2(1,0),
①若 ,
,
∴
②若AB与x轴不垂直,设直线AB的斜率为k,则AB的方程为y=k(x+1)
由 …………(*)
…………(*)
 方程(*)有两个不同的实根.
方程(*)有两个不同的实根.
设点A(x1,y1),B(x2,y2),则x1,x2是方程(*)的两个根





由①②知
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com