题目列表(包括答案和解析)
数列{
}的前n项和为
，
（Ⅰ）设
，证明：数列｛
｝是等比数列；
（Ⅱ）求数列
的前n项和
；
（Ⅲ）若
，
，
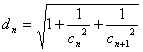，求不超过P的最大整数的值。
设数列｛a
｝的首项a
=1,前n项和S满足关系式：3tS-(2t+3)S
=3t(t>0,n=2,3,4…).(1)求证：数列｛a｝是等比数列；(2)设数列｛a｝的公比为f(t),若数列｛b｝满足：b=1,b=f(
)(n=2,3,4…),求
;(3) 对于（2）中的数列｛b｝，求bb
-bb
+bb
-…+(-1)
bb
的和。
将数列｛an｝中的所有项按每一行比上一行多一项的规则排成如下数表：
a1
a2 a3
a4 a5 a6
a7 a8 a9 a10
……
记表中的第一列数a1，a2，a4，a7，…构成的数列为｛bn｝,b1=a1=1.
Sn为数列｛bn｝的前n项和，且满足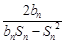
=1（n≥2）.
(Ⅰ)证明数列｛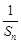
｝成等差数列，并求数列｛bn｝的通项公式；
（Ⅱ）上表中，若从第三行起，每一行中的数按从左到右的顺序均构成等比数列，且公比为同一个正数.当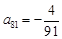
时，求上表中第k(k≥3)行所有项的和．
｝的首项a
=1,前n项和S满足关系式：3tS-(2t+3)S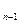
=3t(t>0,n=2,3,4…).(1)求证：数列｛a｝是等比数列；(2)设数列｛a｝的公比为f(t),若数列｛b｝满足：b=1,b=f(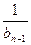
)(n=2,3,4…),求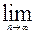
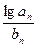;(3) 对于（2）中的数列｛b｝，求bb
-bb
+bb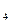
-…+(-1)
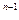bb
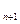的和。设数列{
}的首项
，前
项和S
满足关系式
(其中
=1，2，3，4，…)．
(Ⅰ)求证：数列{}是等比数列；
(Ⅱ)设数列{}的公比为
，作数列｛
｝，使
，(=2，3，4，…)，求数列{}的通项公式；
(Ⅲ)求和：
．
Ⅰ选择题
1.C 2. B 3. B 4.B 5.A 6.C 7.A 8.C 9.D 10.A 11.C 12.C
Ⅱ非选择题
13. 
14. 
15.
16. (2) (3)
17. 解: 
(4分)
(1)增区间为： 
, 减区间为：
(8分)
(2)
(12分)
18.解：因骰子是均匀的，所以骰子各面朝下的可能性相等，设其中一枚骰子朝下的面上的数字为x，另一枚骰子朝下的面上的数字为y，则
的取值如下表：
x+y y
x
1
2
3
5
1
2
3
4
6
2
3
4
5
7
3
4
5
6
8
5
6
7
8
10
从表中可得：
(8分)
(2)p(
=奇数)
………………12分
19.解：(1)
∴
(2分)
又 
恒成立 ∴
∴
∴
∴
(6分)
(2)
∴
∴ ①)当 
时, 解集为
②当 
时,解集为
③当 
时,解集为
(12分)
20.解：PD⊥面ABCD ∴DA、DC、DP 相互垂直
建立如图所示空间直角坐标系Oxyz
(1)
∴
∴
∴PC⊥DA ， PC⊥DE
∴PC⊥面ADE （4分）
（2）∵PD⊥面ABCD PC⊥平面ADE
∴PD与PC夹角为所求
∴ 所求二面角E-AD-B的大小为
（8分）
(3)由(2)得:四边形ADFE为直角梯形，且 EF=1，DF=
，AD=2
∴ 
∴ 所求部分体积 
(12分)
21.解：(1）
为等比数列 
(4分）
（2）
（6分）
(3)
(7分)
(10分)
∴M≥6 (12分)
22.解:(1)直线AB的方程为:
与抛物线的切点设为T
且
∴
∴抛物线c的方程为： 
(3分)
⑵设直线l的方程为
:
易如:
设
，
①M为AN中点 
由 (Ⅰ)、(Ⅱ)联解，得 
代入(Ⅱ)
4
∴直线l的方程为 : 
(7分)
②
(9分)
FM为∠NFA的平分线
且
(11分)
又
(14分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com