题目列表(包括答案和解析)
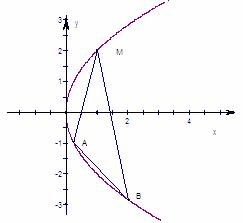
（本小题满分14分）过抛物线C:
上一点
作倾斜角互补的两条直线,分别与抛物线交于A、B两点。
（1）求证：直线AB的斜率为定值；
（2）已知
两点均在抛物线
：
上，若△
的面积的最大值为6，求抛物线的方程。
（本小题满分14分）过抛物线C:
上一点
作倾斜角互补的两条直线,分别与抛物线交于A、B两点。
（1）求证：直线AB的斜率为定值；
（2）已知
两点均在抛物线
：
上，若△
的面积的最大值为6，求抛物线的方程。
（本小题满分14分）已知
，点
在
轴上，点
在
轴的正半轴，点
在直线
上，且满足
，
. w.w.w.k.s.5.u.c.o.m 
（Ⅰ）当点在轴上移动时，求动点的轨迹
方程；
的直线
与轨迹交于
、
两点，又过、作轨迹的切线
、
，当
，求直线的方程.（本小题满分14分）
如图，已知圆
：
是椭圆
的内接△
的内切圆，其中
为椭圆的左顶点。
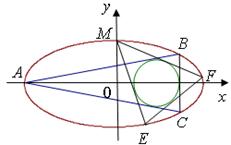
（1）求圆
的半径
；
（2）过点
作圆的两条切线交椭圆于
两点，证明：直线
与圆相切。
（本小题满分14分）
设
，椭圆方程为
，抛物线方程为
．如图6所示，过点
作
轴的平行线，与抛物线在第一象限的交点为
，已知抛物线在点的切线经过椭圆的右焦点
．
（1）求满足条件的椭圆方程和抛物线方程；
（2）设
分别是椭圆长轴的左、右端点，试探究在抛物线上是否存在点
，使得
为直角三角形？若存在，请指出共有几个这样的点？并说明理由（不必具体求出这些点的坐标）．
Ⅰ选择题
1.C 2. B 3. B 4.B 5.A 6.C 7.A 8.C 9.D 10.A 11.C 12.C
Ⅱ非选择题
13. 
14. 
15.
16. (2) (3)
17. 解: 
(4分)
(1)增区间为： 
, 减区间为：
(8分)
(2)
(12分)
18.解：因骰子是均匀的，所以骰子各面朝下的可能性相等，设其中一枚骰子朝下的面上的数字为x，另一枚骰子朝下的面上的数字为y，则
的取值如下表：
x+y y
x
1
2
3
5
1
2
3
4
6
2
3
4
5
7
3
4
5
6
8
5
6
7
8
10
从表中可得：
(8分)
(2)p(
=奇数)
………………12分
19.解：(1)
∴
(2分)
又 
恒成立 ∴
∴
∴
∴
(6分)
(2)
∴
∴ ①)当 
时, 解集为
②当 
时,解集为
③当 
时,解集为
(12分)
20.解：PD⊥面ABCD ∴DA、DC、DP 相互垂直
建立如图所示空间直角坐标系Oxyz
(1)
∴
∴
∴PC⊥DA ， PC⊥DE
∴PC⊥面ADE （4分）
（2）∵PD⊥面ABCD PC⊥平面ADE
∴PD与PC夹角为所求
∴ 所求二面角E-AD-B的大小为
（8分）
(3)由(2)得:四边形ADFE为直角梯形，且 EF=1，DF=
，AD=2
∴ 
∴ 所求部分体积 
(12分)
21.解：(1）
为等比数列 
(4分）
（2）
（6分）
(3)
(7分)
(10分)
∴M≥6 (12分)
22.解:(1)直线AB的方程为:
与抛物线的切点设为T
且
∴
∴抛物线c的方程为： 
(3分)
⑵设直线l的方程为
:
易如:
设
，
①M为AN中点 
由 (Ⅰ)、(Ⅱ)联解，得 
代入(Ⅱ)
4
∴直线l的方程为 : 
(7分)
②
(9分)
FM为∠NFA的平分线
且
(11分)
又
(14分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com