
题目列表(包括答案和解析)
(本题满分12分)
已知向量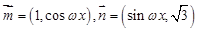
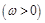 ,函数
,函数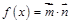 ,且
,且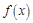 图象上一个最高点的坐标为
图象上一个最高点的坐标为 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为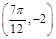 .
.
(Ⅰ)求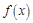 的解析式;
的解析式;
(Ⅱ)在△ABC中,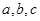 是角A、B、C所对的边,且满足
是角A、B、C所对的边,且满足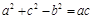 ,求角B的大小以及
,求角B的大小以及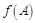 的取值范围.
的取值范围.
(本题满分12分)
已知向量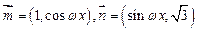
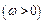 ,函数
,函数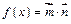 ,且
,且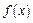 图象上一个最高点的坐标为
图象上一个最高点的坐标为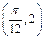 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为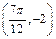 .
.
(Ⅰ)求
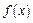 的解析式;
的解析式;
(Ⅱ)在△ABC中,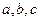 是角A、B、C所对的边,且满足
是角A、B、C所对的边,且满足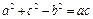 ,求角B的大小以及
,求角B的大小以及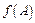 的取值范围.
的取值范围.
(本题满分12分)如图所示,F1、F2是双曲线x2 – y2 = 1的两个焦点,O为坐标原点,
圆O是以F??1F2为直径的圆,直线l:y = kx + b与圆O相切,并与双曲线交于A、B两点.
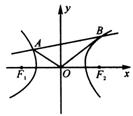 (Ⅰ)根据条件求出b和k的关系式;
(Ⅰ)根据条件求出b和k的关系式;
(Ⅱ)当![]() ,且满足2≤m≤4时,
,且满足2≤m≤4时,
求△AOB面积的取值范围.
(本题满分12分)
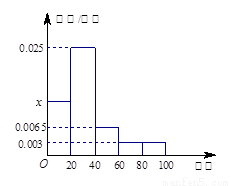
某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率直方图(如图),其中,上学所需时间的范围是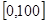 ,样本数据分组为
,样本数据分组为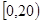 ,
,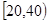 ,
,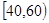 ,
,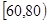 ,
,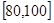 .
.
(Ⅰ)求直方图中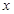 的值;
的值;
(Ⅱ)如果上学所需时间不小于1小时的学生中可以申请在学校住宿,请估计学校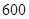
名新生中有多少名学生可以住宿.
(本题满分12分)
某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率直方图(如图),其中,上学所需时间的范围是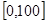 ,样本数据分组为
,样本数据分组为 ,
, ,
,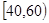 ,
, ,
, .
.
(Ⅰ)求直方图中 的值;
的值;
(Ⅱ)如果上学所需时间不小于1小时的学生中可以申请在学校住宿,请估计学校
名新生中有多少名学生可以住宿.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com