
题目列表(包括答案和解析)
| y2 |
| a2 |
| x2 |
| b2 |
| PA |
| OA |
| PB |
| OB |
| 25 |
| 3 |
| a2 | ||
|
|
| b2 | ||
|
|
| 25 |
| 16 |
| PA |
| PB |
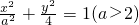 上一点P到它的左右两个焦点的距离和是6,
上一点P到它的左右两个焦点的距离和是6,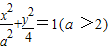 上一点P到它的左右两个焦点的距离和是6,
上一点P到它的左右两个焦点的距离和是6,椭圆 的方程为
的方程为 ,离心率为
,离心率为 ,且短轴一端点和两焦点构成的三角形面积为1,抛物线
,且短轴一端点和两焦点构成的三角形面积为1,抛物线 的方程为
的方程为 ,抛物线的焦点F与椭圆的一个顶点重合.
,抛物线的焦点F与椭圆的一个顶点重合.
(1)求椭圆 和抛物线
和抛物线 的方程;
的方程;
(2)过点F的直线交抛物线 于不同两点A,B,交y轴于点N,已知
于不同两点A,B,交y轴于点N,已知 的值.
的值.
(3)直线 交椭圆
交椭圆 于不同两点P,Q,P,Q在x轴上的射影分别为P′,Q′,满足
于不同两点P,Q,P,Q在x轴上的射影分别为P′,Q′,满足 (O为原点),若点S满足
(O为原点),若点S满足 ,判定点S是否在椭圆
,判定点S是否在椭圆 上,并说明理由.
上,并说明理由.
椭圆C: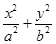 =1(a>b>0)的左、右焦点分别是F1、F2,离心率为
=1(a>b>0)的左、右焦点分别是F1、F2,离心率为 ,过F1且垂直于x轴的直线被椭圆C截得的线段长为1.
,过F1且垂直于x轴的直线被椭圆C截得的线段长为1.
(1)求椭圆C的方程;
(2)点P是椭圆C上除长轴端点外的任一点,过点P作斜率为k的直线l,使得l与椭圆C有且只有一个公共点.设直线PF1,PF2的斜率分别为k1,k2.若k≠0,试证明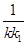 +
+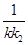 为定值,并求出这个定值.
为定值,并求出这个定值.
1.D 2.B 3.C 4.B 5.A 6.D 7.C 8.C 9.B 10.A
11. 数学文科.files/image204.gif) 12.40 13.
12.40 13. 数学文科.files/image206.gif) 14.
14.数学文科.files/image208.gif) 15.
15.数学文科.files/image210.gif) ; 5
16
; 5
16 数学文科.files/image212.gif)
数学文科.files/image214.jpg)
18.(1)数学文科.files/image216.gif)
(2)由乘法原理解题,甲先抽有5种可能,后乙抽有4种可能,故所有可能的抽法为数学文科.files/image218.gif) 种,即基本事件的总数为20,而甲抽红,乙抽红只有两种可能,所以
种,即基本事件的总数为20,而甲抽红,乙抽红只有两种可能,所以数学文科.files/image220.gif)
(3)由(2)知总数依然20,而甲抽到白色有3种,乙抽红色有2种,由乘法原理基本事件应为3×2=6,所以数学文科.files/image222.gif)
(4)(法一)同(1)乙与甲无论谁先抽,抽到任何一张的概率均等,所以数学文科.files/image224.gif)
(法二)利用互斥事件和,甲红,乙红+甲白,乙红,
所以数学文科.files/image226.gif)
数学文科.files/image228.gif)
数学文科.files/image224.gif)
19. 解:(1)数学文科.files/image231.gif)
数学文科.files/image233.gif) 时,
时,数学文科.files/image235.gif) 取得最小值
取得最小值数学文科.files/image237.gif) ,
,
即数学文科.files/image239.gif)
(2)令数学文科.files/image241.gif)
由数学文科.files/image243.gif) ,得
,得数学文科.files/image245.gif) 或
或数学文科.files/image247.gif) (舍去)
(舍去)
数学文科.files/image249.gif)
(0,1)
1
(1,2)
数学文科.files/image251.gif)
数学文科.files/image253.gif)
0
数学文科.files/image255.gif)
数学文科.files/image257.gif)
增
极大值数学文科.files/image259.gif)
减
数学文科.files/image261.gif) 在
在数学文科.files/image263.gif) 内有最大值
内有最大值数学文科.files/image259.gif) ,
,
数学文科.files/image266.gif) 对
对数学文科.files/image178.gif) 时恒成立等价于
时恒成立等价于数学文科.files/image269.gif) 恒成立。
恒成立。
即数学文科.files/image271.gif)
数学文科.files/image273.gif)
20.证明
(1)取PO中点H,连FH,AH则FH平行且等于数学文科.files/image081.gif) CD,又CD平行且等于AB,E为AB中点,
CD,又CD平行且等于AB,E为AB中点,数学文科.files/image228.gif) FH平行且等于AE
FH平行且等于AE数学文科.files/image228.gif) AEFH为平行四边形,从而EF∥AH,又EF
AEFH为平行四边形,从而EF∥AH,又EF数学文科.files/image276.gif) 平面PAD,AH
平面PAD,AH数学文科.files/image278.gif) 平面PAD,所以EF∥平面PAD
平面PAD,所以EF∥平面PAD
(2) 数学文科.files/image280.gif) PA⊥平面ABCD,
PA⊥平面ABCD,数学文科.files/image228.gif) PA⊥CD,又CD⊥AD
PA⊥CD,又CD⊥AD数学文科.files/image228.gif) CD⊥平面PAD,又AH
CD⊥平面PAD,又AH数学文科.files/image278.gif) 平面PAD,
平面PAD, 数学文科.files/image228.gif) CD⊥AH,而AH∥EF,
CD⊥AH,而AH∥EF,数学文科.files/image228.gif) CD⊥EF.
CD⊥EF.
(3)由CD⊥平面PAD,CD∥AB,数学文科.files/image228.gif) BA⊥平面PAD,
BA⊥平面PAD, 数学文科.files/image228.gif) BA⊥AH, BA⊥DA,
BA⊥AH, BA⊥DA, 数学文科.files/image228.gif)
数学文科.files/image282.gif) 即为二面角F―AB―C的平面角,由PA=AB=AD,易知
即为二面角F―AB―C的平面角,由PA=AB=AD,易知数学文科.files/image282.gif) =
=数学文科.files/image284.gif) ,即为二面角F―AB―C的度数是
,即为二面角F―AB―C的度数是数学文科.files/image284.gif)
数学文科.files/image286.jpg)
21.解:(1)在等比数列数学文科.files/image184.gif) 中,前
中,前数学文科.files/image186.gif) 项和为
项和为数学文科.files/image188.gif) ,若
,若数学文科.files/image192.gif) 成等差数列,则
成等差数列,则数学文科.files/image190.gif) 成等差数列。
成等差数列。
(2)数列数学文科.files/image184.gif) 的首项为
的首项为数学文科.files/image288.gif) ,公比为
,公比为数学文科.files/image290.gif) 。由题意知:
。由题意知:数学文科.files/image292.gif)
即数学文科.files/image294.gif)
数学文科.files/image296.gif)
当数学文科.files/image298.gif) 时,有
时,有数学文科.files/image300.gif)
显然:数学文科.files/image302.gif) 。此时逆命题为假。
。此时逆命题为假。
当数学文科.files/image304.gif) 时,有
时,有数学文科.files/image306.gif) ,
,
数学文科.files/image308.gif)
数学文科.files/image310.gif) ,此时逆命题为真。
,此时逆命题为真。
22.(1)数学文科.files/image312.gif) 与之有共同焦点的椭圆可设为
与之有共同焦点的椭圆可设为数学文科.files/image314.gif) 代入(2,―3)点,
代入(2,―3)点,
解得m=10或m=―2(舍),故所求方程为数学文科.files/image316.gif)
(2)
1、若数学文科.files/image318.gif)
则数学文科.files/image320.gif) 于是
于是数学文科.files/image322.gif)
2、若数学文科.files/image324.gif) ,则
,则数学文科.files/image326.gif)
数学文科.files/image328.gif) △< 0
△< 0数学文科.files/image228.gif) 无解即这样的三角形不存在,综合1,2知
无解即这样的三角形不存在,综合1,2知数学文科.files/image322.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com