
题目列表(包括答案和解析)
已知数列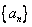 的前
的前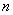 项和为
项和为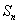 ,点
,点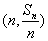 在直线
在直线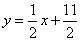 上,数列
上,数列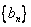 满足
满足 ,
,
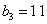 ,且
,且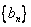 的前9项和为153.
的前9项和为153.
(1)求数列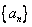 和
和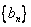 的通项公式;
的通项公式;
(2)设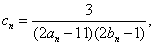 记数列
记数列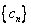 的前
的前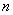 项和为
项和为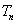 ,求使不等式
,求使不等式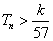 对一切
对一切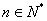 都成立的最大正整数
都成立的最大正整数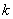 的值.
的值.
数列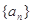 的前n项和记为
的前n项和记为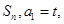 点
点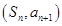 在直线
在直线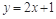 上,
上,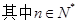 .(1)若数列
.(1)若数列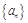 是等比数列,求实数
是等比数列,求实数 的值;
的值;
(2)设各项均不为0的数列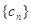 中,所有满足
中,所有满足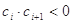 的整数
的整数 的个数称为这个数列
的个数称为这个数列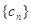 的“积异号数”,令
的“积异号数”,令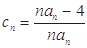 (
(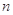
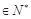 ),在(1)的条件下,求数列
),在(1)的条件下,求数列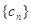 的“积异号数”
的“积异号数”
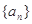 的前n项和记为
的前n项和记为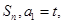 点
点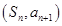 在直线
在直线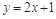 上,
上,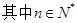 .(1)若数列
.(1)若数列 是等比数列,求实数
是等比数列,求实数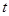 的值;
的值;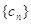 中,所有满足
中,所有满足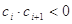 的整数
的整数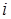 的个数称为这个数列
的个数称为这个数列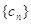 的“积异号数”,令
的“积异号数”,令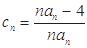 (
(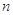
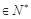 ),在(1)的条件下,求数列
),在(1)的条件下,求数列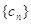 的“积异号数”
的“积异号数”| n+1 |
| 2n |
| 1 |
| 2 |
| a | 2 n |
| 2 |
| an+2 |
| an |
| bn |
| 4+an |
| 1-an |
| 3 |
| 2 |
一、选择题(每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
A
C
D
A
D
B
D
B
B
A
C
二、填空题(每小题5分,共20分)
13、f(x)=2x3-12x
14、.files/image245.gif) 15、2 16、0≤a≤3
15、2 16、0≤a≤3
三、解答题
17(10分).解:原不等式等价于.files/image247.gif) -----------------------------------2分
-----------------------------------2分
当.files/image249.gif) --------------------------------------------4分
--------------------------------------------4分
当.files/image251.gif)
.files/image253.gif)
-------------------------------------------------6分
-------------------------------------------------8分
综上: .files/image255.gif) --------------------------------10分
--------------------------------10分
18(12分). 解:(Ⅰ).files/image072.gif)
.files/image258.gif)
.files/image260.gif)
.files/image262.gif) ----------------3分
----------------3分
.files/image264.gif) -----------------------------4分
-----------------------------4分
令.files/image266.gif) ,
,.files/image268.gif)
.files/image270.gif) 的单调区间为
的单调区间为 .files/image272.gif) ----------------6分
----------------6分
(Ⅱ)由.files/image274.gif) 得
得.files/image276.gif)
.files/image278.gif) ----------7分
----------7分
又.files/image280.gif) 为
为.files/image167.gif) 的内角,
的内角,.files/image283.gif)
.files/image285.gif)
.files/image287.gif) ---------8分
---------8分
.files/image289.gif)
.files/image291.gif)
.files/image293.gif) -------------------10分
-------------------10分
.files/image295.gif)
.files/image297.gif) ------------12分
------------12分
19(12分).解:⑴.files/image299.gif) 对任意的正数
对任意的正数.files/image301.gif) 均有
均有.files/image188.gif) 且
且.files/image190.gif) .
.
又.files/image299.gif)
.files/image306.gif) ----------2分
----------2分
.files/image308.gif)
.files/image310.gif) ,
----------------------------------------4分
,
----------------------------------------4分
又.files/image312.gif) 是定义在
是定义在.files/image314.gif) 上的单调函数,
上的单调函数,.files/image308.gif)
.files/image317.gif) . ----------6分
. ----------6分
(2)当.files/image319.gif) 时,
时,.files/image321.gif) ,
,.files/image323.gif) .
..files/image325.gif) ,
,.files/image327.gif) .----------8分
.----------8分
当.files/image329.gif) 时,
时,.files/image331.gif) ,
,
.files/image333.gif) .
----------------------------------------10分
.
----------------------------------------10分
.files/image335.gif) ,
,.files/image337.gif) 为等差数列.
为等差数列.
.files/image339.gif) ,
,.files/image341.gif) .
-----------------------------------------12分
.
-----------------------------------------12分
20(12分). (1)y==
t=2-cosx ∵x∈[0,) ∴t∈[1,2) -----------------------------------------3分
∴y===t+ -1
∵y=t+ -1在t∈[1,2)上为增函数 ∴y∈[1,) 即M=[1,) 6分
(2)由(x-a-1)(2a-x)>0即 (x-a-1)(x-2a)<0 ∵a<1∴2a<a+1 ∴N=(2a,a+1) 8分
又∁UM=(-∞,1)∪[,+∞) 10分
要使N⊆∁UM,需a+1≤1或2a≥,得 a≤0或 a≥. 12分
21(12分).解:对函数.files/image216.gif) 求导,得
求导,得
.files/image343.gif)
.files/image345.gif) ----------------------------2分
----------------------------2分
令.files/image347.gif) 解得
解得 .files/image349.gif) 或
或.files/image351.gif)
当.files/image160.gif) 变化时,
变化时,.files/image354.gif) 、
、.files/image216.gif) 的变化情况如下表:
的变化情况如下表:
x
0
.files/image357.gif)
.files/image359.gif)
.files/image361.gif)
.files/image363.gif)
.files/image354.gif)
.files/image365.gif)
0
.files/image367.gif)
.files/image216.gif)
.files/image369.gif)
减函数
.files/image371.gif)
增函数
.files/image373.gif)
----------------------4分
所以,当.files/image375.gif) 时,
时,.files/image216.gif) 是减函数;当
是减函数;当.files/image378.gif) 时,
时,.files/image216.gif) 是增函数;
是增函数;
当.files/image380.gif) 时,
时,.files/image216.gif) 的值域为
的值域为.files/image382.gif) ----------------------------6分
----------------------------6分
(Ⅱ)对函数.files/image384.gif) 求导,得
求导,得
.files/image386.gif)
因此.files/image218.gif) ,当
,当.files/image380.gif) 时,
时,.files/image390.gif)
因此当.files/image392.gif) ,g(x)为减函数,从而当
,g(x)为减函数,从而当.files/image392.gif) 时有个g(x)
时有个g(x).files/image395.gif)
又g(1)=.files/image397.gif)
.files/image399.gif) ----------------8分
----------------8分
若对于任意.files/image222.gif) ,
,.files/image401.gif) ,存在
,存在.files/image224.gif) ,使得
,使得.files/image226.gif) ,则
,则
[.files/image243.gif)
.files/image403.gif) ]
].files/image405.gif)
即.files/image407.gif) ----------------------------------------10分
----------------------------------------10分
解.files/image409.gif) 式得
式得 .files/image218.gif) 或
或.files/image412.gif)
解.files/image414.gif) 式得
式得 .files/image416.gif)
又.files/image218.gif) ,
,
故:.files/image140.gif) 的取值范围为
的取值范围为.files/image419.gif) -----------------------------------12分
-----------------------------------12分
22(12分). :(1)∵Sn=2an ?n ∴Sn+1=2an+1 ?(n+1) 两式相减得, an+1=2an+1----------------2分
数列{an+λ}是等比数列 即: an+1+λ=2(an+λ),∴λ=1.
∵a1=s1=2a1-1,∴a1=1
∵数列{ an+1}是首项为2,公比为2的等比数列 ------------------------4分
∴an+1=(a1+1)2n-1=2n,∴an=2n -1 ------------------------6分
(2)∵an=2n -1
∴bn ====-----------------10分
∴Tn=(-)+(-)+…+(-)=1-<1. ----------------12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com