
题目列表(包括答案和解析)
对于使![]() 成立的所有常数
成立的所有常数![]() 中,我们把
中,我们把![]() 的最小值
的最小值![]() 叫做
叫做![]() 的上确界,若
的上确界,若![]() ,则
,则![]() 的上确界为( ) .
的上确界为( ) .
(![]() )-3 (
)-3 (![]() )
)![]() (
(![]() )-
)-![]() (
(![]() )
)![]()
对于使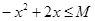 成立的所有常数
成立的所有常数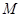 中,我们把
中,我们把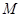 的最小值1叫做
的最小值1叫做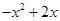 的上确界,若
的上确界,若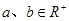 ,且
,且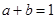 ,则
,则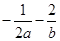 的上确界为( )
的上确界为( )
A.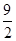 B.
B.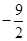 C.
C.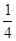 D.-4
D.-4
对于使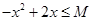 成立的所有常数
成立的所有常数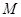 中,我们把
中,我们把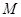 的最小值
的最小值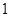 叫做
叫做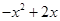 的上确界,若
的上确界,若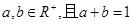 ,则
,则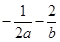 的上确界为 ( )
的上确界为 ( )
A.-3
B. 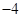 C.-
C.-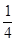 D.
D.
对于使 成立的所有常数
成立的所有常数 中,我们把
中,我们把 的最小值1叫做
的最小值1叫做
的上确界,若 ,且
,且 ,则
,则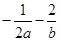 的上确界为(
)
的上确界为(
)
A. B.
B. C.
C. D.-4
D.-4
对于使 成立的所有常数
成立的所有常数 中,我们把
中,我们把 的最小值1叫做
的最小值1叫做 的上确界,若
的上确界,若 ,且
,且 ,则
,则 的上确界为(
)
的上确界为(
)
A.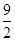 B.
B. C.
C. D.-4
D.-4
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
A
B
D
D
C
A
A
B
A
C
D
一、
填空题13. ; 14.
; 14. ; 15.
; 15. ;16.
;16.
 ,即
,即 ,当m为整数时,值为0,m为小数时,值为-1,故所求值域为{-1,0}
,当m为整数时,值为0,m为小数时,值为-1,故所求值域为{-1,0}
三、解答题
17.(1)

 两两相互垂直, 连结
两两相互垂直, 连结 并延长交
并延长交 于F.
于F.



同理可得


 ,
,  …… (6分)
…… (6分)
(2) 是
是 的重心
的重心
F是SB的中点

 梯形的高
梯形的高
 ,
, .…… (12分)
.…… (12分)
【注】可以用空间向量的方法.
18.(1) .…………4分
.…………4分
(2)若该天订购 束鲜花,则盈利为
束鲜花,则盈利为 元;
元;
若该天订购 束鲜花,盈利为
束鲜花,盈利为 ,则其分布列为
,则其分布列为






 (元).
(元).
若该天订购 束鲜花,盈利为
束鲜花,盈利为 ,则其分布列为
,则其分布列为








 (元).
(元).
综上可知,该花店这一天应订购 束鲜花盈利最大. …………12分
束鲜花盈利最大. …………12分
19.(1) .
.
又
 .
.

 .………6分
.………6分
(2)


又 ,
,
 .从而
.从而

当 且同向时,
且同向时, .………12分
.………12分
20.(1)当 时,
时, ,
, ,令
,令 .
.
列表分析:













故 在
在 上满足
上满足 ,从而
,从而 .
.
设 ,
, ,令
,令 ,
, 在
在 上为减函数,故
上为减函数,故 ,由于
,由于  ,从而
,从而 .……6分
.……6分
(2) .
.
①若 ,则
,则 ,
, ,
, ,令
,令 ,矛盾.
,矛盾.
②若 ,令
,令 .
.












 ,令
,令 .
.
③若 ,则
,则 ,
, ,令
,令 ,得
,得 (舍去).
(舍去).
综合①②③知 . ……12分
. ……12分
21.(1)设抛物线方程为 ,
,
由

∴ ,∴抛物线方程为
,∴抛物线方程为 ;
;
 …………4分
…………4分
(2)依题意,可设直线 的方程为
的方程为  代入抛物线方程
代入抛物线方程 得
得
 ①
①
设 两点的坐标分别是
两点的坐标分别是  、
、 、
、 是方程①的两根.…………6分
是方程①的两根.…………6分
所以 
由点 分有向线段
分有向线段 所成的比为
所成的比为 ,得
,得
又点 与点
与点 关于原点对称,故点
关于原点对称,故点 的坐标是
的坐标是 ,从而
,从而 .
.
 ……7分
……7分


 所以
所以  …………8分
…………8分
(3)设
 ,
,
 ,
, ,∵
,∵ ,
,
∴ 的方程为
的方程为
 ;
;
∵ 过
过 ,∴
,∴ ,同理
,同理
∴ 为方程
为方程 的两个根;∴
的两个根;∴ ;……11分
;……11分
又 ,∴
,∴ 的方程为
的方程为
∴ ,显然直线
,显然直线 过点
过点 ……12分
……12分
22.(1) ……4分
……4分
(2)由 ,而
,而 ,
, ,
,  ,
, ,
,
 恒成立,
恒成立, ,
, ,即
,即 .……8分
.……8分
(3) 由(2)得当 时知
时知 ,
, ,设数列
,设数列 ,
, ,
,
 .
.
 ,
, ,故
,故 ,
, ,
,
 ,
, ,
,
即 ………14分
………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com