
题目列表(包括答案和解析)
(本小题满分12分)
如图1,在三棱锥P-A.BC中,PA.⊥平面A.BC,A.C⊥BC,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示.

(1) 证明:A.D⊥平面PBC;
(2) 求三棱锥D-A.BC的体积;
(3) 在∠A.CB的平分线上确定一点Q,使得PQ∥平面A.BD,并求此时PQ的长.
(本小题满分12分) 如图4,正三棱柱
如图4,正三棱柱![]() 中,
中,![]() ,
,![]() 、
、![]() 分别是侧棱
分别是侧棱![]() 、
、![]() 上的点,且使得折线
上的点,且使得折线![]() 的长
的长![]() 最短.
最短.
(1)证明:平面![]() 平面
平面![]() ;(2)求直线
;(2)求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
(本小题满分12分)如图,已知三棱柱 的侧棱与底面垂直,
的侧棱与底面垂直, ,
,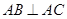 ,
, ,
, 分别是
分别是 ,
,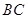 的中点,点
的中点,点 在直线
在直线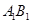 上,且
上,且 ;
;
(1)证明:无论 取何值,总有
取何值,总有 ;
;
(2)当 取何值时,直线
取何值时,直线 与平面
与平面 所成的角
所成的角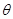 最大?并求该角取最大值时的正切值;
最大?并求该角取最大值时的正切值;
(3)是否存在点 ,使得平面
,使得平面 与平面
与平面 所成的二面角为30º,若存在,试确定点
所成的二面角为30º,若存在,试确定点 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.

(本小题满分12分)
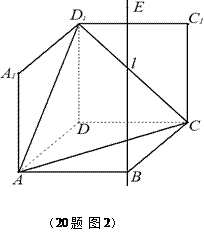
如图1,在平面内,ABCD边长为2的正方形,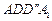 和
和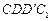 都是正方形。将两个正方形分别沿AD,CD折
都是正方形。将两个正方形分别沿AD,CD折 起,使
起,使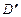 与
与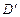 重合于点D1。设直线l过点B且垂直于正方形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面A
重合于点D1。设直线l过点B且垂直于正方形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面A BCD同侧,设
BCD同侧,设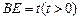 (图2)。
(图2)。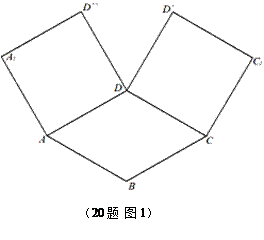
(1)设二面角E – AC – D1的大小为q,当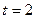 时,求
时,求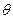 的余弦值;
的余弦值;
(2)当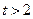 时在线段
时在线段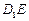 上是否存在点
上是否存在点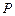 ,使平面
,使平面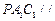 平面
平面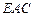 ,若存在,求出
,若存在,求出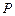 分
分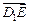 所成的比
所成的比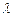 ;若不存在,请说明理由。
;若不存在,请说明理由。
(本小题满分12分)
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(I)求出该几何体的体积;
(II)求证:EM∥平面ABC;
|
 ? 若存在,确定点N的位置; 若不存在,请说明理由.
? 若存在,确定点N的位置; 若不存在,请说明理由.
一、选择题

二、填空题
13. ; 14.112; 15.
; 14.112; 15. ; 16.
; 16.
三、解答题
17.解:∵向量 的夹角
的夹角 ,
,

①当 时,
时, ;②当
;②当 时,
时, ;③当
;③当 时,
时,

综上所述:当 时,
时,  的范围是
的范围是 当
当 时,
时, 的范围是
的范围是 ;
;
当 时,
时,  的范围是
的范围是
18.解:(1) ∵ 底面ABC,∴
底面ABC,∴ .又∵
.又∵ 是正三角形,且E为AC的中点,
是正三角形,且E为AC的中点, .又
.又 ,
, 平面PAC.
平面PAC. 平面PEF,
平面PEF,
∴平面 平面PAC.
平面PAC.
(2)取CD的中点F,则点F即为所求.∵E、F分别为CA、CD的中点, .
.
又 平面PEF,
平面PEF, 平面PEF,∴
平面PEF,∴ 平面PEF.
平面PEF.
(3) .
.
19.解:(1)

依题意
 ,
,




(2)
又
在Rt△ABC中,

又
20.解:(I) ,
,
由 ,
,  ,
,
 ,
,
 ,
, ,∴
,∴ 。
。
(II)由 得:
得:
 ,
,
 ,
, ,
,
由②-①得:

 。
。
21解:当年生产x(万件)时,
年生产成本=固定费用+年生产费用 ,
,
年销售收入 ,∵利润=销售收入―生产成本―促销费,
,∵利润=销售收入―生产成本―促销费,
∴

 (万元).
(万元).
当切仅当 即
即 时,
时,
∴该企业2008年的促销费投入7万元时,企业的年利润 (万元)最大.
(万元)最大.
22.解:(1)依题意: ∵
∵ 上是增函数,
上是增函数,
∴ 恒成立,
恒成立,
∴ ∵
∵ ∴b的取值范围为
∴b的取值范围为
(2)设 则函数化为
则函数化为 ,
,
∵ ∴当
∴当 上为增函数,
上为增函数,
当 时,
时, 当
当
 当
当 上为减函数,
上为减函数,
当 时,
时, 综上所述,当
综上所述,当
当 时,
时, ;
;
(3)设点P、Q的坐标是
则点M、N的横坐标为 C1在M处的切线斜率为
C1在M处的切线斜率为
C2在点N处的切线斜率
假设C1在点M处的切线与C2在点N处的切线平行,则
即 则
则




 。设
。设 。
。
令 则
则
∵ ∴
∴ 所以
所以 上单调递增,故
上单调递增,故 ,则
,则 这与①矛盾,假设不成立,故C1在点M处的切线与C2在点N处的切线不平行。
这与①矛盾,假设不成立,故C1在点M处的切线与C2在点N处的切线不平行。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com