
题目列表(包括答案和解析)
(本小题满分12分)
已知函数![]() 的图像都过点P(2,0),且在点P处
的图像都过点P(2,0),且在点P处
有相同的切线。
(I)求实数a、b、c的值;
(II)设函数![]() 上的最小值。
上的最小值。
(本小题满分12分)
已知函数![]() 的图象过点
的图象过点![]() ,且在点
,且在点![]() 处的切线方程为
处的切线方程为![]() . 求函数
. 求函数![]() 的解析式
的解析式
(本小题满分12分)
已知函数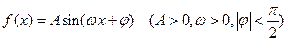 的图象与
的图象与 轴的交点为
轴的交点为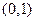 ,它在
,它在 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为 和
和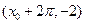 .
.
(1)求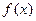 的解析式;
的解析式;
(2)若锐角 满足
满足 ,求
,求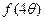 的值.
的值.
(本小题满分12分)
已知函数 的图象过点
的图象过点 ,且图象上与点P最近的一个最低点是
,且图象上与点P最近的一个最低点是 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若 ,且
,且 为第三象限的角,求
为第三象限的角,求 的值;
的值;
(Ⅲ)若 在区间
在区间 上有零点,求
上有零点,求 的取值范围.
的取值范围.
(本小题满分12分)
已知函数
 的图象过点
的图象过点 .
.
(Ⅰ)求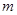 的值;
的值;
(Ⅱ)在△ 中,角
中,角 ,
, ,
, 的对边分别是
的对边分别是 ,
, ,
, .若
.若 ,求
,求 的取值范围.
的取值范围.
一、选择题

二、填空题
13. ; 14.112; 15.
; 14.112; 15. ; 16.
; 16.
三、解答题
17.解:∵向量 的夹角
的夹角 ,
,

①当 时,
时, ;②当
;②当 时,
时, ;③当
;③当 时,
时,

综上所述:当 时,
时,  的范围是
的范围是 当
当 时,
时, 的范围是
的范围是 ;
;
当 时,
时,  的范围是
的范围是
18.解:(1) ∵ 底面ABC,∴
底面ABC,∴ .又∵
.又∵ 是正三角形,且E为AC的中点,
是正三角形,且E为AC的中点, .又
.又 ,
, 平面PAC.
平面PAC. 平面PEF,
平面PEF,
∴平面 平面PAC.
平面PAC.
(2)取CD的中点F,则点F即为所求.∵E、F分别为CA、CD的中点, .
.
又 平面PEF,
平面PEF, 平面PEF,∴
平面PEF,∴ 平面PEF.
平面PEF.
(3) .
.
19.解:(1)

依题意
 ,
,




(2)
又
在Rt△ABC中,

又
20.解:(I) ,
,
由 ,
,  ,
,
 ,
,
 ,
, ,∴
,∴ 。
。
(II)由 得:
得:
 ,
,
 ,
, ,
,
由②-①得:

 。
。
21解:当年生产x(万件)时,
年生产成本=固定费用+年生产费用 ,
,
年销售收入 ,∵利润=销售收入―生产成本―促销费,
,∵利润=销售收入―生产成本―促销费,
∴

 (万元).
(万元).
当切仅当 即
即 时,
时,
∴该企业2008年的促销费投入7万元时,企业的年利润 (万元)最大.
(万元)最大.
22.解:(1)依题意: ∵
∵ 上是增函数,
上是增函数,
∴ 恒成立,
恒成立,
∴ ∵
∵ ∴b的取值范围为
∴b的取值范围为
(2)设 则函数化为
则函数化为 ,
,
∵ ∴当
∴当 上为增函数,
上为增函数,
当 时,
时, 当
当
 当
当 上为减函数,
上为减函数,
当 时,
时, 综上所述,当
综上所述,当
当 时,
时, ;
;
(3)设点P、Q的坐标是
则点M、N的横坐标为 C1在M处的切线斜率为
C1在M处的切线斜率为
C2在点N处的切线斜率
假设C1在点M处的切线与C2在点N处的切线平行,则
即 则
则




 。设
。设 。
。
令 则
则
∵ ∴
∴ 所以
所以 上单调递增,故
上单调递增,故 ,则
,则 这与①矛盾,假设不成立,故C1在点M处的切线与C2在点N处的切线不平行。
这与①矛盾,假设不成立,故C1在点M处的切线与C2在点N处的切线不平行。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com