
题目列表(包括答案和解析)
| 休闲方式 性别 |
看电视 | 看书 | 合计 |
| 男 | 10 | 50 | 60 |
| 女 | 10 | 10 | 20 |
| 合计 | 20 | 60 | 80 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥K0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| K0 | 2.072 | 2.706 | 3.841 | 5.042 | 6.635 |
(本小题12分)
随机调查某社区80个人,以研究这一社区居民在20:00-22:00时间段的休闲方式与性别有关系,得到下面的数据表:
|
休闲方式 性别 |
看电视 |
看书 |
合计 |
|
男 |
10 |
50 |
60 |
|
女 |
10 |
10 |
20 |
|
合计 |
20 |
60 |
80 |
(1)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量 ,求
,求 的分布列和期望;
的分布列和期望;
(2)根据以上数据,能否有99%的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?
参考公式:  ,其中
,其中
参考数据:
|
|
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
|
|
2.072 |
2.706 |
3.841 |
5.042 |
6.635 |
(本小题12分)
随机调查某社区80个人,以研究这一社区居民在20:00-22:00时间段的休闲方式与性别有关系,得到下面的数据表:
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 10 | 50 | 60 |
| 女 | 10 | 10 | 20 |
| 合计 | 20 | 60 | 80 |
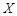 ,求
,求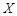 的分布列和期望;
的分布列和期望;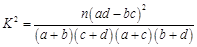 ,其中
,其中
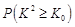 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
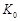 | 2.072 | 2.706 | 3.841 | 5.042 | 6.635 |
为调查某社区居民的业余生活状况,研究这一社区居民在20:00-22:00时间段的休闲方式与性别的关系,随机调查了该社区80人,得到下面的数据表:
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 10 | 50 | 60 |
| 女 | 10 | 10 | 20 |
| 合计 | 20 | 60 | 80 |
 ,其中n=a+b+c+d.
,其中n=a+b+c+d.| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
| 休闲方式 性别 |
看电视 | 看书 | 合计 |
| 男 | 10 | 50 | 60 |
| 女 | 10 | 10 | 20 |
| 合计 | 20 | 60 | 80 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥K0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| K0 | 2.072 | 2.706 | 3.841 | 5.042 | 6.635 |
说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.
2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
4.只给整数分数,选择题和填空题不给中间分.
一、选择题:本大题主要考查基本知识和基本运算.共10小题,每小题5分,满分50分.
题号
1
2
3
4
5
6
7
8
9
10
答案
C
A
B
A
B
C
D
C
B
D
二、填空题:本大题主要考查基本知识和基本运算.本大题共5小题,考生作答4小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题.
11.1.files/image234.gif) 12.
12.1.files/image236.gif) 13.
13.1.files/image238.gif) 14.
14.1.files/image240.gif) 15.2
15.2
说明:第14题答案可以有多种形式,如可答1.files/image242.gif) 或
或1.files/image244.gif) Z)等, 均给满分.
Z)等, 均给满分.
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
解:(1)∵1.files/image246.gif)
1.files/image248.gif) …… 2分
…… 2分
1.files/image250.gif) …… 4分
…… 4分
1.files/image252.gif) .
…… 6分
.
…… 6分
∴1.files/image254.gif) .
…… 8分
.
…… 8分
(2) 当1.files/image256.gif) 时,
时, 1.files/image040.gif) 取得最大值, 其值为2 .
……10分
取得最大值, 其值为2 .
……10分
此时1.files/image259.gif) ,即
,即1.files/image261.gif)
1.files/image263.gif) Z
Z1.files/image144.gif) .
……12分
.
……12分
17. (本小题满分12分)
解:(1) 由频率分布条形图知,抽取的学生总数为1.files/image266.gif) 人. ……4分
人. ……4分
∵各班被抽取的学生人数成等差数列,设其公差为1.files/image268.gif) ,
,
由1.files/image270.gif) =100,解得
=100,解得1.files/image272.gif) .
.
∴各班被抽取的学生人数分别是22人,24人,26人,28人. ……8分
(2) 在抽取的学生中,任取一名学生, 则分数不小于90分的概率为0.35+0.25+0.1+0.05=0.75.
……12分
18.(本小题满分14分)
解:(1)∵ 1.files/image159.gif) ⊥平面
⊥平面1.files/image161.gif) ,
,1.files/image173.gif)
1.files/image277.gif) 平面
平面1.files/image161.gif) ,
,
∴
1.files/image159.gif) ⊥
⊥1.files/image173.gif) . …… 2分
. …… 2分
∵
1.files/image173.gif) ⊥
⊥1.files/image282.gif) ,
,1.files/image159.gif)
1.files/image284.gif)
1.files/image282.gif)
1.files/image287.gif) ,
,
∴
1.files/image173.gif) ⊥平面
⊥平面1.files/image289.gif) ,
…… 4分
,
…… 4分
∵
1.files/image175.gif)
1.files/image277.gif) 平面
平面1.files/image289.gif) ,
,
∴
1.files/image173.gif) ⊥
⊥1.files/image175.gif) .
…… 6分
.
…… 6分
1.files/image294.gif) (2)法1: 取线段
(2)法1: 取线段1.files/image177.gif) 的中点
的中点1.files/image179.gif) ,
,1.files/image298.gif) 的中点
的中点1.files/image300.gif) ,连结
,连结1.files/image302.gif) ,
,
则1.files/image304.gif) 是△
是△1.files/image306.gif) 中位线.
中位线.
∴1.files/image304.gif) ∥
∥1.files/image309.gif) ,
,1.files/image311.gif) ,
……8分
,
……8分
∵
1.files/image164.gif) ,
,1.files/image314.gif) ,
,
∴1.files/image316.gif) .
.
∴
四边形1.files/image318.gif) 是平行四边形,
……10分
是平行四边形,
……10分
∴ 1.files/image320.gif) .
.
∵ 1.files/image181.gif)
1.files/image323.gif) 平面
平面1.files/image132.gif) ,
,1.files/image326.gif)
1.files/image277.gif) 平面
平面1.files/image132.gif) ,
,
∴ 1.files/image181.gif) ∥平面
∥平面1.files/image132.gif) .
……12分
.
……12分
∴
线段1.files/image177.gif) 的中点
的中点1.files/image179.gif) 是符合题意要求的点.
……14分
是符合题意要求的点.
……14分
法2: 取线段1.files/image177.gif) 的中点
的中点1.files/image179.gif) ,
,1.files/image309.gif) 的中点
的中点1.files/image300.gif) ,连结
,连结1.files/image333.gif) ,
,
1.files/image335.gif) 则
则1.files/image304.gif) 是△
是△1.files/image306.gif) 的中位线.
的中位线.
∴1.files/image304.gif) ∥
∥1.files/image298.gif) ,
,1.files/image338.gif) ,
,
∵1.files/image340.gif) 平面
平面1.files/image132.gif) ,
, 1.files/image343.gif) 平面
平面1.files/image132.gif) ,
,
∴1.files/image346.gif) 平面
平面1.files/image132.gif) .
…… 8分
.
…… 8分
∵
1.files/image164.gif) ,
,1.files/image314.gif) ,
,
∴1.files/image350.gif) .
.
∴
四边形1.files/image352.gif) 是平行四边形,
是平行四边形,
∴ 1.files/image354.gif) .
.
∵ 1.files/image356.gif)
1.files/image323.gif) 平面
平面1.files/image132.gif) ,
,1.files/image359.gif)
1.files/image277.gif) 平面
平面1.files/image132.gif) ,
,
∴ 1.files/image356.gif) ∥平面
∥平面1.files/image363.gif) .
……10分
.
……10分
∵1.files/image365.gif) ,
,
∴平面1.files/image367.gif) 平面
平面1.files/image132.gif) .
.
∵1.files/image370.gif) 平面
平面1.files/image372.gif) ,
,
∴1.files/image181.gif) ∥平面
∥平面1.files/image132.gif) .
……12分
.
……12分
∴
线段1.files/image177.gif) 的中点
的中点1.files/image179.gif) 是符合题意要求的点.
……14分
是符合题意要求的点.
……14分
19. (本小题满分14分)
解:(1)依题意知,1.files/image375.gif) …… 2分
…… 2分
∵1.files/image377.gif) ,
,
∴1.files/image379.gif) .
…… 4分
.
…… 4分
∴所求椭圆1.files/image086.gif) 的方程为
的方程为1.files/image381.gif) .
…… 6分
.
…… 6分
(2)∵ 点1.files/image125.gif)
1.files/image197.gif) 关于直线
关于直线1.files/image199.gif) 的对称点为
的对称点为1.files/image201.gif) ,
,
∴ 1.files/image384.gif) …… 8分
…… 8分
解得:1.files/image386.gif) ,
,1.files/image388.gif) .
…… 10分
.
…… 10分
∴1.files/image390.gif) .
…… 12分
.
…… 12分
∵
点1.files/image125.gif)
1.files/image197.gif) 在椭圆
在椭圆1.files/image086.gif) :
:1.files/image381.gif) 上,
上,
∴1.files/image392.gif) , 则
, 则1.files/image394.gif) .
.
∴1.files/image203.gif) 的取值范围为
的取值范围为1.files/image397.gif) .
……14分
.
……14分
20. (本小题满分14分)
(1) 解:当1.files/image399.gif) 时,
时,1.files/image401.gif) .
……1分
.
……1分
当1.files/image403.gif) 时,
时,1.files/image405.gif)
1.files/image407.gif)
1.files/image409.gif) .
……3分
.
……3分
∵1.files/image411.gif) 不适合上式,
不适合上式,
∴1.files/image413.gif) ……4分
……4分
(2)证明: ∵1.files/image415.gif) .
.
当1.files/image417.gif) 时,
时,1.files/image419.gif) ……6分
……6分
当1.files/image403.gif) 时,
时,1.files/image422.gif) ,
①
,
①
1.files/image424.gif) . ②
. ②
①-②得:
1.files/image426.gif)
1.files/image428.gif)
得1.files/image430.gif) ,
……8分
,
……8分
此式当1.files/image417.gif) 时也适合.
时也适合.
∴1.files/image432.gif) N
N1.files/image434.gif) .
.
∵1.files/image436.gif) ,
,
∴1.files/image438.gif) .
……10分
.
……10分
当1.files/image403.gif) 时,
时,1.files/image440.gif) ,
,
∴1.files/image442.gif) .
……12分
.
……12分
∵1.files/image444.gif) ,
,
∴1.files/image446.gif) .
.
故1.files/image448.gif) ,即
,即1.files/image450.gif) .
.
综上,1.files/image452.gif) .
……14分
.
……14分
21. (本小题满分14分)
解:(1)当1.files/image228.gif) 时,
时,1.files/image455.gif) ,
,
∴1.files/image457.gif)
1.files/image459.gif) .
.
令1.files/image457.gif) =0, 得
=0, 得 1.files/image461.gif) . …… 2分
. …… 2分
当1.files/image463.gif) 时,
时,1.files/image465.gif) , 则
, 则1.files/image230.gif) 在
在1.files/image468.gif) 上单调递增;
上单调递增;
当1.files/image470.gif) 时,
时,1.files/image472.gif) , 则
, 则1.files/image230.gif) 在
在1.files/image474.gif) 上单调递减;
上单调递减;
当1.files/image476.gif) 时,
时,1.files/image465.gif) ,
, 1.files/image230.gif) 在
在1.files/image478.gif) 上单调递增.
…… 4分
上单调递增.
…… 4分
∴ 当1.files/image480.gif) 时,
时, 1.files/image230.gif) 取得极大值为
取得极大值为1.files/image483.gif)
1.files/image485.gif) ;
;
当1.files/image487.gif) 时,
时, 1.files/image230.gif) 取得极小值为
取得极小值为1.files/image490.gif)
1.files/image492.gif) . …… 6分
. …… 6分
(2) ∵ 1.files/image457.gif) =
= 1.files/image494.gif) ,
,
∴△= 1.files/image496.gif) =
= 1.files/image498.gif) .
.
① 若a≥1,则△≤0, …… 7分
∴1.files/image457.gif) ≥0在R上恒成立,
≥0在R上恒成立,
∴ f(x)在R上单调递增 .
∵f(0)1.files/image500.gif) ,
,1.files/image502.gif) ,
,
∴当a≥1时,函数f(x)的图象与x轴有且只有一个交点. …… 9分
② 若a<1,则△>0,
∴1.files/image457.gif) = 0有两个不相等的实数根,不妨设为x1,x2,(x1<x2).
= 0有两个不相等的实数根,不妨设为x1,x2,(x1<x2).
∴x1+x2 = 2,x1x2 = a.
当1.files/image018.gif) 变化时,
变化时,1.files/image505.gif) 的取值情况如下表:
的取值情况如下表:
x
1.files/image507.gif)
x1
(x1,x2)
x2
1.files/image509.gif)
1.files/image457.gif)
+
0
-
0
+
f(x)
ㄊ
极大值
ㄋ
极小值
ㄊ
…… 11分
∵1.files/image511.gif) ,
,
∴1.files/image513.gif) .
.
∴1.files/image515.gif)
1.files/image168.gif)
1.files/image518.gif)
1.files/image520.gif)
1.files/image522.gif) .
.
同理1.files/image524.gif)
1.files/image526.gif) .
.
∴1.files/image528.gif)
1.files/image530.gif)
1.files/image532.gif)
1.files/image534.gif) .
.
令f(x1)?f(x2)>0, 解得a>1.files/image536.gif) .
.
而当1.files/image538.gif) 时,
时,1.files/image540.gif) ,
,
故当1.files/image538.gif) 时, 函数f(x)的图象与x轴有且只有一个交点. …… 13分
时, 函数f(x)的图象与x轴有且只有一个交点. …… 13分
综上所述,a的取值范围是1.files/image542.gif) .
…… 14分
.
…… 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com