
题目列表(包括答案和解析)
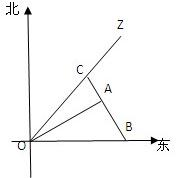 如图,一科学考察船从港口O出发,沿北偏东a角的射线OZ方向航行,其中tana=
如图,一科学考察船从港口O出发,沿北偏东a角的射线OZ方向航行,其中tana=| 1 |
| 3 |
| 13 |
| 2 | ||
|
 ,在距离港口O为3
,在距离港口O为3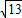 a(a为正常数)海里北偏东β角的A处有一个供科学考察船物资的小岛,其中cosβ=
a(a为正常数)海里北偏东β角的A处有一个供科学考察船物资的小岛,其中cosβ=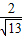 ,现指挥部紧急征调沿海岸线港口O正东方向m海里的B处的补给船,速往小岛A装运物资供给科学考察船,该船沿BA方向不变追赶科学考察船,并在C处相遇.经测算,当两船运行的航线OZ与海岸线OB围成三角形OBC的面积S最小时,补给最合适.
,现指挥部紧急征调沿海岸线港口O正东方向m海里的B处的补给船,速往小岛A装运物资供给科学考察船,该船沿BA方向不变追赶科学考察船,并在C处相遇.经测算,当两船运行的航线OZ与海岸线OB围成三角形OBC的面积S最小时,补给最合适.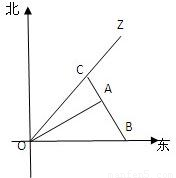
 ,在距离港口O为3
,在距离港口O为3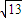 a(a为正常数)海里北偏东β角的A处有一个供科学考察船物资的小岛,其中cosβ=
a(a为正常数)海里北偏东β角的A处有一个供科学考察船物资的小岛,其中cosβ=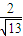 ,现指挥部紧急征调沿海岸线港口O正东方向m海里的B处的补给船,速往小岛A装运物资供给科学考察船,该船沿BA方向不变追赶科学考察船,并在C处相遇.经测算,当两船运行的航线OZ与海岸线OB围成三角形OBC的面积S最小时,补给最合适.
,现指挥部紧急征调沿海岸线港口O正东方向m海里的B处的补给船,速往小岛A装运物资供给科学考察船,该船沿BA方向不变追赶科学考察船,并在C处相遇.经测算,当两船运行的航线OZ与海岸线OB围成三角形OBC的面积S最小时,补给最合适.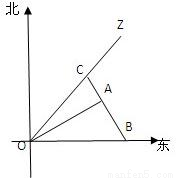
 ,在距离港口O为3
,在距离港口O为3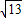 a(a为正常数)海里北偏东β角的A处有一个供科学考察船物资的小岛,其中cosβ=
a(a为正常数)海里北偏东β角的A处有一个供科学考察船物资的小岛,其中cosβ=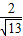 ,现指挥部紧急征调沿海岸线港口O正东方向m海里的B处的补给船,速往小岛A装运物资供给科学考察船,该船沿BA方向不变追赶科学考察船,并在C处相遇.经测算,当两船运行的航线OZ与海岸线OB围成三角形OBC的面积S最小时,补给最合适.
,现指挥部紧急征调沿海岸线港口O正东方向m海里的B处的补给船,速往小岛A装运物资供给科学考察船,该船沿BA方向不变追赶科学考察船,并在C处相遇.经测算,当两船运行的航线OZ与海岸线OB围成三角形OBC的面积S最小时,补给最合适.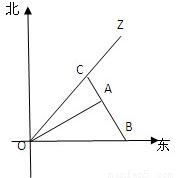
例10 为促进个人住房商品化的进程,我国1999年元月公布了个人住房公积金贷款利率和商业性贷款利率如下:
贷款期(年数)
公积金贷款月利率(‰)
商业性贷款月利率(‰)
……
11
12
13
14
15
……
……
4.365
4.455
4.545
4.635
4.725
……
……
5.025
5.025
5.025
5.025
5.025
……
汪先生家要购买一套商品房,计划贷款25万元,其中公积金贷款10万元,分十二年还清;商业贷款15万元,分十五年还清.每种贷款分别按月等额还款,问:
(1)汪先生家每月应还款多少元?
(2)在第十二年底汪先生家还清了公积金贷款,如果他想把余下的商业贷款也一次性还清;那么他家在这个月的还款总数是多少?
(参考数据:1.004455144=1.8966,1.005025144=2.0581,1.005025180=2.4651)
讲解 设月利率为r,每月还款数为a元,总贷款数为A元,还款期限为n月
第1月末欠款数 A(1+r)-a
第2月末欠款数 [A(1+r)-a](1+r)-a= A(1+r)2-a (1+r)-a
第3月末欠款数 [A(1+r)2-a (1+r)-a](1+r)-a
=A(1+r)3-a (1+r)2-a(1+r)-a
……
第n月末欠款数
得:
对于12年期的10万元贷款,n=144,r=4.455‰
∴
对于15年期的15万元贷款,n=180,r=5.025‰
∴
由此可知,汪先生家前12年每月还款942.37+1268.22=2210.59元,后3年每月还款1268.22元.
(2)至12年末,汪先生家按计划还款以后还欠商业贷款
其中A=150000,a=1268.22,r=5.025‰ ∴X=41669.53
再加上当月的计划还款数2210.59元,当月共还款43880.12元.
需要提及的是,本题的计算如果不许用计算器,就要用到二项展开式进行估算,这在2002年全国高考第(12)题中得到考查.
例11 医学上为研究传染病传播中病毒细胞的发展规律及其预防,将病毒细胞注入一只小白鼠体内进行实验,经检测,病毒细胞的增长数与天数的关系记录如下表. 已知该种病毒细胞在小白鼠体内的个数超过108的时候小白鼠将死亡.但注射某种药物,将可杀死其体内该病毒细胞的98%.
(1)为了使小白鼠在实验过程中不死亡,第一次最迟应在何时注射该种药物?(精确到天)
(2)第二次最迟应在何时注射该种药物,才能维持小白鼠的生命?(精确到天)
已知:lg2=0.3010.
讲解 (1)由题意病毒细胞关于时间n的函数为, 则由
两边取对数得 n27.5,
即第一次最迟应在第27天注射该种药物.
(2)由题意注入药物后小白鼠体内剩余的病毒细胞为,
再经过x天后小白鼠体内病毒细胞为,
由题意≤108,两边取对数得
,
故再经过6天必须注射药物,即第二次应在第33天注射药物.
本题反映的解题技巧是“两边取对数”,这对实施指数运算是很有效的.
例12 有一个受到污染的湖泊,其湖水的容积为V立方米,每天流出湖泊的水量都是r立方米,现假设下雨和蒸发正好平衡,且污染物质与湖水能很好地混合,用g(t)表示某一时刻t每立方米湖水所含污染物质的克数,我们称为在时刻t时的湖水污染质量分数,已知目前污染源以每天p克的污染物质污染湖水,湖水污染质量分数满足关系式g(t)= +[g(0)- ]?e(p≥0),其中,g(0)是湖水污染的初始质量分数.
(1)当湖水污染质量分数为常数时,求湖水污染的初始质量分数;
(2)求证:当g(0)< 时,湖泊的污染程度将越来越严重;
(3)如果政府加大治污力度,使得湖泊的所有污染停止,那么需要经过多少天才能使湖水的污染水平下降到开始时污染水平的5%?
讲解(1)∵g(t)为常数, 有g(0)-=0, ∴g(0)= .
(2) 我们易证得0<t1<t2, 则
g(t1)-g(t2)=[g(0)- ]e-[g(0)- ]e=[g(0)- ][e-e]=[g(0)- ],
∵g(0)?<0,t1<t2,e>e,
∴g(t1)<g(t2) .
故湖水污染质量分数随时间变化而增加,污染越来越严重.
(3)污染停止即P=0,g(t)=g(0)?e,设经过t天能使湖水污染下降到初始污染水平5%即g(t)=5% g(0)?
∴=e,∴t= ln20,
故需要 ln20天才能使湖水的污染水平下降到开始时污染水平的5%.
高考应用性问题的热门话题是增减比率型和方案优化型, 另外,估测计算型和信息迁移型也时有出现.当然,数学高考应用性问题关注当前国内外的政治,经济,文化, 紧扣时代的主旋律,凸显了学科综合的特色,是历年高考命题的一道亮丽的风景线.
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com