
题目列表(包括答案和解析)
在平面直角坐标系 中,曲线
中,曲线 与坐标轴的交点都在圆
与坐标轴的交点都在圆 上.
上.
(1)求圆 的方程;
的方程;
(2)若圆 与直线
与直线 交于
交于 、
、 两点,且
两点,且 ,求
,求 的值.
的值.
【解析】本试题主要是考查了直线与圆的位置关系的运用。
(1)曲线 与
与 轴的交点为(0,1),
轴的交点为(0,1),
与 轴的交点为(3+2
轴的交点为(3+2 ,0),(3-2
,0),(3-2 ,0) 故可设
,0) 故可设 的圆心为(3,t),则有32+(t-1)2=(2
的圆心为(3,t),则有32+(t-1)2=(2 )2+t2,解得t=1.
)2+t2,解得t=1.
(2)因为圆 与直线
与直线 交于
交于 、
、 两点,且
两点,且 。联立方程组得到结论。
。联立方程组得到结论。
求圆心在直线y=-2x上,并且经过点A(2,-1),与直线x+y=1相切的圆的方程.
【解析】利用圆心和半径表示圆的方程,首先
设圆心为S,则KSA=1,∴SA的方程为:y+1=x-2,即y=x-3, ………4分
和y=-2x联立解得x=1,y=-2,即圆心(1,-2)
∴r= =
= ,
,
故所求圆的方程为: +
+ =2
=2
解:法一:
设圆心为S,则KSA=1,∴SA的方程为:y+1=x-2,即y=x-3, ………4分
和y=-2x联立解得x=1,y=-2,即圆心(1,-2) ……………………8分
∴r= =
= ,
………………………10分
,
………………………10分
故所求圆的方程为: +
+ =2
………………………12分
=2
………………………12分
法二:由条件设所求圆的方程为: +
+ =
=
 , ………………………6分
, ………………………6分
解得a=1,b=-2,  =2
………………………10分
=2
………………………10分
所求圆的方程为: +
+ =2
………………………12分
=2
………………………12分
其它方法相应给分
在△ABC中,a、b、c分别是角A、B、C的对边,cosB= .
.
⑴ 若cosA=- ,求cosC的值; ⑵
若AC=
,求cosC的值; ⑵
若AC= ,BC=5,求△ABC的面积.
,BC=5,求△ABC的面积.
【解析】第一问中sinB=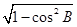 =
= , sinA=
, sinA= =
=
cosC=cos(180°-A-B)=-cos(A+B) =sinA.sinB-cosA·cosB
= ×
× -(-
-(- )×
)× =
=
第二问中,由 =
= +
+ -2AB×BC×cosB得 10=
-2AB×BC×cosB得 10= +25-8AB
+25-8AB
解得AB=5或AB=3综合得△ABC的面积为 或
或
解:⑴ sinB=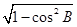 =
= , sinA=
, sinA= =
= ,………………2分
,………………2分
∴cosC=cos(180°-A-B)=-cos(A+B) ……………………3分
=sinA.sinB-cosA·cosB ……………………4分
= ×
× -(-
-(- )×
)× =
= ……………………6分
……………………6分
⑵ 由 =
= +
+ -2AB×BC×cosB得 10=
-2AB×BC×cosB得 10= +25-8AB
………………7分
+25-8AB
………………7分
解得AB=5或AB=3, ……………………9分
若AB=5,则S△ABC= AB×BC×sinB=
AB×BC×sinB= ×5×5×
×5×5× =
= ………………10分
………………10分
若AB=3,则S△ABC= AB×BC×sinB=
AB×BC×sinB= ×5×3×
×5×3× =
= ……………………11分
……………………11分
综合得△ABC的面积为 或
或
已知 是等差数列,其前n项和为Sn,
是等差数列,其前n项和为Sn, 是等比数列,且
是等比数列,且 ,
, .
.
(Ⅰ)求数列 与
与 的通项公式;
的通项公式;
(Ⅱ)记 ,
, ,证明
,证明 (
( ).
).
【解析】(1)设等差数列 的公差为d,等比数列
的公差为d,等比数列 的公比为q.
的公比为q.
由 ,得
,得 ,
, ,
, .
.
由条件,得方程组 ,解得
,解得
所以 ,
, ,
, .
.
(2)证明:(方法一)
由(1)得
 ①
①
 ②
②
由②-①得



而
故 ,
,
(方法二:数学归纳法)
① 当n=1时,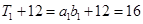 ,
, ,故等式成立.
,故等式成立.
② 假设当n=k时等式成立,即 ,则当n=k+1时,有:
,则当n=k+1时,有:






即 ,因此n=k+1时等式也成立
,因此n=k+1时等式也成立
由①和②,可知对任意 ,
, 成立.
成立.
已知 ,且
,且 .
.
(1)求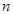 的值;
的值;
(2)求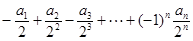 的值.
的值.
【解析】本试题主要考查了二项式定理的运用,以及系数求和的赋值思想的运用。第一问中,因为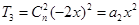 ,所以
,所以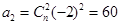 ,可得
,可得 ,第二问中,因为
,第二问中,因为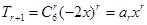 ,所以
,所以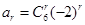 ,所以
,所以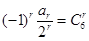 ,利用组合数性质可知。
,利用组合数性质可知。
解:(1)因为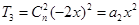 ,所以
,所以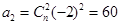 , ……3分
, ……3分
化简可得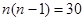 ,且
,且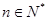 ,解得
,解得 . …………6分
. …………6分
(2)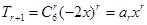 ,所以
,所以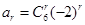 ,
,
所以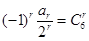 ,
,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com