因为，所以点P为线段AC的中点，所以应该选B。

答案：B。

【命题立意】:本题考查了向量的加法运算和平行四边形法则，可以借助图形解答。

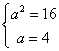∵,,∴∴,故选D.

答案:D

【命题立意】:本题考查了集合的并集运算,并用观察法得到相对应的元素,从而求得答案,本题属于容易题.

下列是真命题的命题序号是     .

①分别表示空间向量的有向线段所在的直线是异面直线，则这两个向量不是共面向量

②若|a|=|b|，则a，b的长度相等而方向相同或相反

③若向量，满足||＞||，且与同向，则＞

④若两个非零向量与满足+=，则∥

A.分别表示空间向量的有向线段所在的直线是异面直线，则这两个向量不是共面向量

B.若|a|=|b|,则a、b的长度相等而方向相同或相反

C.若向量、满足||＞||,且与同向，则＞

D.若两个非零向量与满足+=0，则∥

A.分别表示空间向量的有向线段所在的直线是异面直线，则这两个向量不是共面向量

B.若|a|=|b|,则a，b的长度相等而方向相同或相反

C.若向量，满足||＞||，且与同向，则＞

D.若两个非零向量与满足+=0，则∥