
题目列表(包括答案和解析)
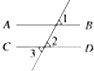 如图,因为AB∥CD,所以∠1=∠2,又因为∠2+∠3=180°,所以∠1+∠3=180°.所用的推理规则为( )
如图,因为AB∥CD,所以∠1=∠2,又因为∠2+∠3=180°,所以∠1+∠3=180°.所用的推理规则为( )4. m>2或m<-2 解析:因为f(x)=![]() 在(-1,1)内有零点,所以f(-1)f(1)<0,即(2+m)(2-m)<0,则m>2或m<-2
在(-1,1)内有零点,所以f(-1)f(1)<0,即(2+m)(2-m)<0,则m>2或m<-2
随机变量![]() 的所有等可能取值为1,2…,n,若
的所有等可能取值为1,2…,n,若![]() ,则( )
,则( )
A. n=3 B.n=4 C. n=5 D.不能确定
5.m=-3,n=2 解析:因为![]() 的两零点分别是1与2,所以
的两零点分别是1与2,所以![]() ,即
,即![]() ,解得
,解得![]()
6.![]() 解析:因为
解析:因为![]() 只有一个零点,所以方程
只有一个零点,所以方程![]() 只有一个根,因此
只有一个根,因此![]() ,所以
,所以![]()
设A是如下形式的2行3列的数表,
|
a |
b |
c |
|
d |
e |
f |
满足性质P:a,b,c,d,e,f ,且a+b+c+d+e+f=0
,且a+b+c+d+e+f=0
记 为A的第i行各数之和(i=1,2),
为A的第i行各数之和(i=1,2),  为A的第j列各数之和(j=1,2,3)记
为A的第j列各数之和(j=1,2,3)记 为
为 中的最小值。
中的最小值。
(1)对如下表A,求 的值
的值
|
1 |
1 |
-0.8 |
|
0.1 |
-0.3 |
-1 |
(2)设数表A形如
|
1 |
1 |
-1-2d |
|
d |
d |
-1 |
其中 ,求
,求 的最大值
的最大值
(3)对所有满足性质P的2行3列的数表A,求 的最大值。
的最大值。
【解析】(1)因为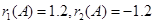 ,
, ,所以
,所以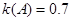
(2)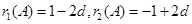 ,
,
因为 ,所以
,所以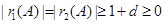 ,
,
所以
当d=0时, 取得最大值1
取得最大值1
(3)任给满足性质P的数表A(如图所示)
|
a |
b |
c |
|
d |
e |
f |
任意改变A的行次序或列次序,或把A中的每个数换成它的相反数,所得数表 仍满足性质P,并且
仍满足性质P,并且 ,因此,不妨设
,因此,不妨设 ,
, ,
,
由 得定义知,
得定义知, ,
, ,
, ,
,
从而

所以, ,由(2)知,存在满足性质P的数表A使
,由(2)知,存在满足性质P的数表A使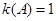 ,故
,故 的最大值为1
的最大值为1
【考点定位】此题作为压轴题难度较大,考查学生分析问题解决问题的能力,考查学生严谨的逻辑思维能力
如图,边长为2的正方形ABCD,E是BC的中点,沿AE,DE将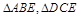 折起,使得B与C重合于O.
折起,使得B与C重合于O.
(Ⅰ)设Q为AE的中点,证明:QD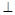 AO;
AO;
(Ⅱ)求二面角O—AE—D的余弦值.
【解析】第一问中,利用线线垂直,得到线面垂直,然后利用性质定理得到线线垂直。取AO中点M,连接MQ,DM,由题意可得:AO EO, DO
EO, DO EO,
EO,
AO=DO=2.AO DM
DM
因为Q为AE的中点,所以MQ//E0,MQ AO
AO
AO 平面DMQ,AO
平面DMQ,AO DQ
DQ
第二问中,作MN AE,垂足为N,连接DN
AE,垂足为N,连接DN
因为AO EO, DO
EO, DO EO,EO
EO,EO 平面AOD,所以EO
平面AOD,所以EO DM
DM
,因为AO DM ,DM
DM ,DM 平面AOE
平面AOE
因为MN AE,DN
AE,DN AE,
AE,  DNM就是所求的DM=
DNM就是所求的DM= ,MN=
,MN=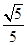 ,DN=
,DN= ,COS
,COS DNM=
DNM=
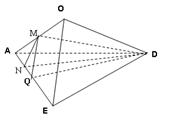
(1)取AO中点M,连接MQ,DM,由题意可得:AO EO, DO
EO, DO EO,
EO,
AO=DO=2.AO DM
DM
因为Q为AE的中点,所以MQ//E0,MQ AO
AO
AO 平面DMQ,AO
平面DMQ,AO DQ
DQ
(2)作MN AE,垂足为N,连接DN
AE,垂足为N,连接DN
因为AO EO, DO
EO, DO EO,EO
EO,EO 平面AOD,所以EO
平面AOD,所以EO DM
DM
,因为AO DM ,DM
DM ,DM 平面AOE
平面AOE
因为MN AE,DN
AE,DN AE,
AE,  DNM就是所求的DM=
DNM就是所求的DM= ,MN=
,MN=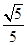 ,DN=
,DN= ,COS
,COS DNM=
DNM=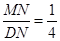
二面角O-AE-D的平面角的余弦值为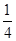
过抛物线

 的对称轴上的定点
的对称轴上的定点 ,作直线
,作直线 与抛物线相交于
与抛物线相交于 两点.
两点.
(I)试证明 两点的纵坐标之积为定值;
两点的纵坐标之积为定值;
(II)若点 是定直线
是定直线 上的任一点,试探索三条直线
上的任一点,试探索三条直线 的斜率之间的关系,并给出证明.
的斜率之间的关系,并给出证明.
【解析】本题主要考查抛物线与直线的位置关系以及发现问题和解决问题的能力.
(1)中证明:设 下证之:设直线AB的方程为: x=ty+m与y2=2px联立得消去x得y2=2pty-2pm=0,由韦达定理得
下证之:设直线AB的方程为: x=ty+m与y2=2px联立得消去x得y2=2pty-2pm=0,由韦达定理得

(2)中:因为三条直线AN,MN,BN的斜率成等差数列,下证之
设点N(-m,n),则直线AN的斜率KAN= ,直线BN的斜率KBN=
,直线BN的斜率KBN=

KAN+KBN= +
+
本题主要考查抛物线与直线的位置关系以及发现问题和解决问题的能力.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com