
题目列表(包括答案和解析)
((本小题满分14分)
给定椭圆 :
:
 ,称圆心在坐标原点
,称圆心在坐标原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 的“伴随圆”.
已知椭圆
的“伴随圆”.
已知椭圆 的两个焦点分别是
的两个焦点分别是 ,椭圆
,椭圆 上一动点
上一动点 满足
满足 .
.
(Ⅰ)求椭圆 及其“伴随圆”的方程
及其“伴随圆”的方程
(Ⅱ)试探究y轴上是否存在点 (0,
(0,  )
) ,使得过点
,使得过点 作直线
作直线 与椭圆
与椭圆 只有一个交点,且
只有一个交点,且 截椭圆
截椭圆 的“伴随圆”所得的弦长为
的“伴随圆”所得的弦长为 .若存在,请求出
.若存在,请求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(本小题满分13分)
给定椭圆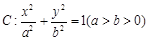 ,称圆心在坐标原点
,称圆心在坐标原点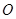 ,半径为
,半径为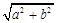 的圆是椭圆
的圆是椭圆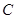 的“伴随圆”. 若椭圆C的一个焦点为
的“伴随圆”. 若椭圆C的一个焦点为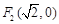 ,其短轴上的一个端点到
,其短轴上的一个端点到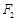 距离为
距离为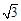 .
.
(Ⅰ)求椭圆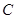 及其“伴随圆”的方程;
及其“伴随圆”的方程;
(Ⅱ)若过点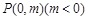 的直线
的直线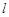 与椭圆C只有一个公共点,且
与椭圆C只有一个公共点,且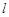 截椭圆C的“伴随圆”所得的弦长为
截椭圆C的“伴随圆”所得的弦长为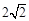 ,求
,求 的值;
的值;
(Ⅲ)过椭圆C“伴椭圆”上一动点Q作直线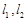 ,使得
,使得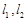 与椭圆C都只有一个公共点,试判断直线
与椭圆C都只有一个公共点,试判断直线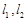 的斜率之积是否为定值,并说明理由.
的斜率之积是否为定值,并说明理由.
给定椭圆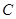 :
:
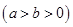 ,称圆心在坐标原点
,称圆心在坐标原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆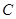 的“伴随圆”. 已知椭圆
的“伴随圆”. 已知椭圆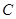 的两个焦点分别是
的两个焦点分别是 ,椭圆
,椭圆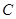 上一动点
上一动点 满足
满足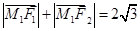 .
.
(Ⅰ)求椭圆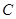 及其“伴随圆”的方程;
及其“伴随圆”的方程;
(Ⅱ)过点P
 作直线
作直线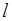 ,使得直线
,使得直线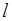 与椭圆
与椭圆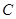 只有一个交点,且
只有一个交点,且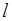 截椭圆
截椭圆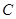 的“伴随圆”所得的弦长为
的“伴随圆”所得的弦长为 .求出
.求出 的值.
的值.
(本小题满分13分)
给定椭圆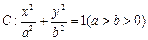 ,称圆心在坐标原点
,称圆心在坐标原点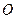 ,半径为
,半径为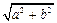 的圆是椭圆
的圆是椭圆 的“伴随圆”. 若椭圆C的一个焦点为
的“伴随圆”. 若椭圆C的一个焦点为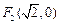 ,其短轴上的一个端点到
,其短轴上的一个端点到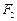 距离为
距离为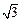 .
.
(Ⅰ)求椭圆 及其“伴随圆”的方程;
及其“伴随圆”的方程;
(Ⅱ)若过点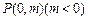 的直线
的直线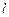 与椭圆C只有一个公共点,且
与椭圆C只有一个公共点,且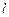 截椭圆C的“伴随圆”所得的弦长为
截椭圆C的“伴随圆”所得的弦长为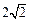 ,求
,求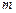 的值;
的值;
(Ⅲ)过椭圆C“伴椭圆”上一动点Q作直线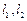 ,使得
,使得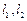 与椭圆C都只有一个公共点,试判断直线
与椭圆C都只有一个公共点,试判断直线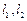 的斜率之积是否为定值,并说明理由.
的斜率之积是否为定值,并说明理由.
(本题满分10分)
已知椭圆 的方程为
的方程为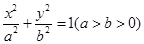 ,称圆心在坐标原点
,称圆心在坐标原点 ,半径为
,半径为 的圆为椭圆
的圆为椭圆 的“伴随圆”,椭圆
的“伴随圆”,椭圆 的短轴长为2,离心率为
的短轴长为2,离心率为 .
.
(Ⅰ)求椭圆 及其“伴随圆”的方程;
及其“伴随圆”的方程;
(Ⅱ)若直线 与椭圆
与椭圆 交于
交于 两点,与其“伴随圆”交于
两点,与其“伴随圆”交于 两点,当
两点,当 时,求△
时,求△ 面积的最大值.
面积的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com