
题目列表(包括答案和解析)
(本小题满分10分)
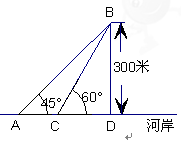
如图,某地海岸线可以近似地看作一条直线,两救生员在岸边A处巡查,发现在海中B处有人求救,救生员甲与乙都没有直接从A处游向B处,甲是沿岸边A处跑到离B最近的D处,然后游向B处;乙是沿岸边A处跑到点C处然后游向B处,若两救生员在岸边的行进速度都为6米∕秒,在海水中的行进速度都为2米∕秒,试分析救生员的选择是否正确?谁先到达点B处?(![]() ,
,![]() )
)
(本小题满分10分)如图,已知反比例函数![]() (
(![]() )的图象与一次函数
)的图象与一次函数![]() 的图象交于
的图象交于![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() ,连接
,连接![]() 平行于
平行于![]() 轴.
轴.
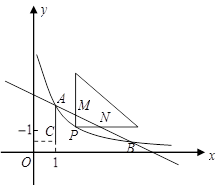
(1)求反比例函数的解析式及点 的坐标.
的坐标.
(2)现有一个直角三角板,让它的直角顶点 在反比例函数图象上的
在反比例函数图象上的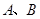 之间的部分滑动(不与
之间的部分滑动(不与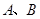 重合),两直角边始终分别平行于
重合),两直角边始终分别平行于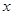 轴、
轴、 轴,且与线段
轴,且与线段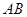 交于
交于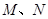 两点,试判断
两点,试判断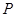 点在滑动过程中
点在滑动过程中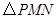 是否与
是否与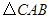 总相似,简要说明判断理由.
总相似,简要说明判断理由.
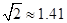 ,
,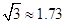 )
)
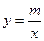 (
(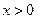 )的图象与一次函数
)的图象与一次函数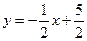 的图象交于
的图象交于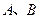 两点,点
两点,点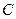 的坐标为
的坐标为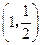 ,连接
,连接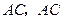 平行于
平行于 轴.
轴.
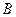 的坐标.
的坐标.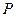 在反比例函数图象上的
在反比例函数图象上的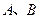 之间的部分滑动(不与
之间的部分滑动(不与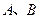 重合),两直角边始终分别平行于
重合),两直角边始终分别平行于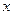 轴、
轴、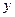 轴,且与线段
轴,且与线段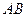 交于
交于 两点,试判断
两点,试判断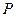 点在滑动过程中
点在滑动过程中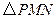 是否与
是否与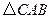 总相似,简要说明判断理由.
总相似,简要说明判断理由.(本小题满分10分)如图,已知反比例函数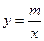 (
(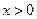 )的图象与一次函数
)的图象与一次函数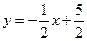 的图象交于
的图象交于 两点,点
两点,点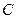 的坐标为
的坐标为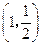 ,连接
,连接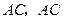 平行于
平行于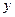 轴.
轴.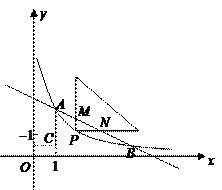
(1)求反比例函数的解析式及点 的坐标.
的坐标.
(2)现有一个直角三角板,让它的直角顶点 在反比例函数图象上的
在反比例函数图象上的 之间的部分滑动(不与
之间的部分滑动(不与 重合),两直角边始终分别平行于
重合),两直角边始终分别平行于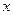 轴、
轴、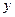 轴,且与线段
轴,且与线段 交于
交于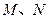 两点,试判断
两点,试判断 点在滑动过程中
点在滑动过程中 是否与
是否与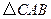 总相似,简要说明判断理由.
总相似,简要说明判断理由.
一 选择题(共20分,每小题2分)
1. B 2 . B 3. C 4 .A 5 C 6 . C 7. C 8. A 9 . B 10. D
.
二,填空题。(共24分,每小题3分)
11 . .files/image117.gif) 12 . 13 .
12 . 13 . .files/image119.gif) 14 .
14 . .files/image121.gif) 15.
15. .files/image123.gif) 16 .
16 . .files/image125.gif) 17 .
17 . .files/image127.gif) 18 .
18 ..files/image129.gif) .
.
三、
.files/image131.gif) 19解:
19解:
当.files/image133.gif) 时,原式=
时,原式=.files/image135.gif) (
(.files/image137.gif) )
)
20(1)如图
.files/image139.gif)
(2)优等人数为 .files/image141.gif)
良等人数为
.files/image143.gif)
(3)优、良等级的概率分别是 .files/image145.gif)
.files/image147.gif)
(4)该校数学成绩优等、良等人数共占40%、.files/image149.gif) 等人数仅占10%,说明该校期末考试成绩比较好.(只要合理,均给分)
等人数仅占10%,说明该校期末考试成绩比较好.(只要合理,均给分)
21.解: (1)∵在Rt△AOB中,∠AOB=900,∠ABO=600,OB=1
.files/image151.jpg) ∴AB=2,OA=
∴AB=2,OA=.files/image153.gif)
∴点A坐标.files/image155.gif)
∵二次函数y=ax2+bx+c的图像经过点A.files/image155.gif) 、点B
、点B.files/image076.gif) 和点C
和点C.files/image078.gif)
∴.files/image157.gif)
.files/image159.gif) 解得
解得.files/image161.gif)
∴该二次函数的表达式.files/image163.gif)
(2)对称轴为.files/image165.gif) ;顶点坐标为
;顶点坐标为.files/image167.gif) .
.
(3)∵对称轴为.files/image165.gif) ,A
,A.files/image155.gif)
∴点D坐标.files/image169.gif)
∴四边形ABCD为等腰梯形
22.解:过点D作DE⊥BC交BC延长线于点E,过点E作EF∥AD交AB于点F
在Rt△CDE中,∠CED=90°,∠DCE=30°,CD=10
∴DE=5, CE=.files/image171.gif)
.files/image173.jpg) ∴BE=
∴BE=.files/image175.gif)
∵太阳光线AD与水平地面成30°角
∴∠FEB=30°
在Rt△BFE中,∠B=90°,∠FEB=30°,BE=.files/image175.gif)
∴BF=BE?tan∠FEB=.files/image177.gif) =
=.files/image179.gif)
∵AF=DE=5
∴AB=AF+BF=.files/image181.gif) =
=.files/image183.gif) =19.1≈19
=19.1≈19
答旗杆AB的高度为19米.
23解:⑴.files/image185.gif)
⑵如图所示
.files/image187.jpg)
.files/image189.gif)
.files/image192.gif) ⑶如图所示
⑶如图所示
.files/image194.gif)
24..files/image196.jpg) 解:(1)如图1,AE=AF. 理由:证明△ABE≌△ADF(ASA)
解:(1)如图1,AE=AF. 理由:证明△ABE≌△ADF(ASA)
(2)如图2, PE=PF.
理由:过点P作PM⊥BC于M,PN⊥DC于N,则PM=PN.由此可证得△PME≌△PNF(ASA),从而证得PE=PF.
(3) PE、PF不具有(2)中的数量关系.
当点P在AC的中点时,PE、PF才具有(2)中的数量关系.
25.解:(1)由已知条件,得
.files/image198.gif)
(2)由已知条件,得
.files/image200.gif)
解得 .files/image202.gif)
.files/image204.gif)
.files/image206.gif)
∴应从A村运到甲库50吨,运到乙库150吨;从B村运到甲库190吨,运到乙库110吨,这样调运就能使总运费最少.
(3)这个同学说的对.
理由:设A村的运费为.files/image208.gif) 元,则
元,则.files/image210.gif) ,
,
.files/image212.gif)
.files/image214.gif)
∴当x=200时,A村的运费最少,
而y=-2x+9680(0≤x≤200)
∵K=-2<0
∴X=200时,y有最小值,两村的总运费也是最少。
即当x=200时,A村和两村的总运费都最少。
26.解:(1)如图,作DE⊥AB于E,CF⊥AB于F,
.files/image216.gif) 依题意可知,四边形CDEF是矩形,AE=BF,
依题意可知,四边形CDEF是矩形,AE=BF,
.files/image218.gif)
在Rt△ADE中,
.files/image220.gif)
∴梯形ABCD的周长为.files/image222.gif) , 面积为
, 面积为.files/image224.gif) .
.
(2)∵PQ平分梯形ABCD的周长,
∴.files/image226.gif)
解得.files/image228.gif)
∴当PQ平分梯形ABCD的周长时,.files/image230.gif)
(3)∵PQ平分梯形ABCD的面积
∴①当点P在AD边上时,.files/image232.gif)
解得.files/image234.gif)
②当点P在DC边上时,
.files/image236.gif) 即
即.files/image238.gif)
解得.files/image240.gif)
③当点P在CB边上时,.files/image242.gif)
∵△<0,∴此方程无解.
∴当PQ平分梯形ABCD的面积时,.files/image244.gif)
(4).files/image246.gif) .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com