若二次函数f(x)=ax2+bx+c(a≠0)的图象和直线y=x无交点,现有下列结论:①方程f(f(x))=x一定没有实数根;

②若a>0,则不等式f(f(x))>x对一切实数x都成立;

③若a<0,则必存在实数x0,使f(f(x0))>x0;

④若a+b+c=0,则不等式f(f(x))<x对一切实数都成立;

⑤函数g(x)=ax2-bx+c的图象与直线y=-x也一定没有交点.

其中正确的结论是　　　　(写出所有正确结论的编号). 

f(x)是(0,+∞)上的非负可导函数,且,对任意正数a,b,若a<b,则(      )

设a,b是非零实数，若a<b,则下列不等式成立的是（   ）

A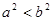                 B．    C．     D．

f()是定义在区间[－c,c]上的奇函数，其图象如图所示：令g（）=af（）+b，则下 列关于函数g（）的叙述正确的是（    ）

A．若a<0,则函数g（）的图象关于原点对称.

B．若a=－1，－2<b<0,则方程g（）=0有大于2的实根.

C．若a≠0,b=2,则方程g（）=0有两个实根.

D．若a≥1,b<2,则方程g（）=0有三个实根

f(x)是(0,+∞)上的非负可导函数,且,对任意正数a,b,若a<b,则(   )