练习册

  • 练习册
  • 试题
    26． 【查看更多】

     

    题目列表(包括答案和解析)

    （本小题满分12分）如图，在平面直角坐标系中，直线：与轴交于点，与轴交于点，抛物线过点、点，且与轴的另一交点为，其中＞0，又点是抛物线的对称轴上一动点．

    （1）求点的坐标，并在图1中的上找一点，使到点与点的距离之和最小；

    （2）若△周长的最小值为，求抛物线的解析式及顶点的坐标；

    （3）如图2，在线段上有一动点以每秒2个单位的速度从点向点移动(不与端点、重合)，过点作∥交轴于点,设移动的时间为秒，试把△的面积表示成时间的函数，当为何值时，有最大值，并求出最大值.

     

    查看答案和解析>>

    （本小题满分12分）

    如图，AB、BC、CD分别与⊙O切于E、F、G，且AB∥CD．连接OB、OC，延长CO交⊙O于点M，过点M作MN ∥OB交CD于N．

    1.⑴求证：MN是⊙O的切线；

    2.⑵当0B=6cm，OC=8cm时，求⊙O的半径及图中阴影部分的面积．

     

    查看答案和解析>>

    （本小题满分12分）

    甲、乙、丙三个人准备打羽毛球，他们约定用“抛硬币”的方式来确定哪两个人先上场，三人手中各持有一枚质地均匀的硬币，同时将手中硬币抛落到水平地面为一个回合．落地后，三枚硬币中，恰有两枚正面向上或反面向上的这两枚硬币持有人先上场；若三枚硬币均为正面向上或反面向上，属于不能确定．

    1.（1）请你画出表示“抛硬币”一个回合所有可能出现的结果的树状图；

    2.（2）求一个回合能确定两人先上场的概率．

     

    查看答案和解析>>

    （本小题满分12分）

    如图，在Rt△OAB中，∠OAB＝90°，且点B的坐标为（4，2）．

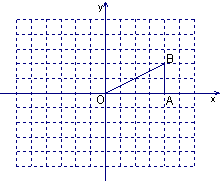
    1.⑴ 画出关于点O成中心对称的，并写出点B1的坐标；

    2.⑵ 求出以点B1为顶点，并经过点B的二次函数关系式．

     

    查看答案和解析>>

     （本小题满分12分）

    如图，RtΔABC中，∠ACB=90°，AC=4，BA=5，点P是AC上的动点（P不与A、C重合）PQ⊥AB，垂足为Q．设PC=x，PQ= y．

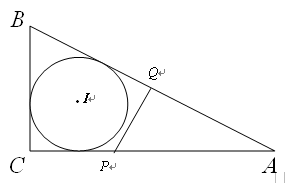
    1.⑴求y与x的函数关系式；

    2.⑵试确定此RtΔABC内切圆I的半径，并探求x为何值时，直线PQ与这个内切圆I相切？

    3.⑶若0<x<1，试判断以P为圆心，半径为y的圆与⊙I能否相内切，若能求出相应的x的值，若不能，请说明理由．

     

    查看答案和解析>>

    一．1．C；  2．C； 3.C；  4．B；  5．Ｄ；  6．B；  7．A； 8．B；  9．A；  10．C。

    二．11．x≥2；   12．1；   13．25°；　　１４．１４５；　　１５．１６；　　

    １６．１８０；　　　１７．①，③；　　　１８．

    三．１９解：原式?????????????????????????????????????????????????????????????????????????? 2分

    ???????????????????????????????????????????????????????????????????????????????????????????? ５分

    当时，原式．??????????????????????????????????????????????????????? ７分．

    ２０．解：（1）（名），

    本次调查了90名学生．?????????????????????????????????????????????????????????????????????????????????????? （2分）

    补全的条形统计图如下：

    文本框: 知道文本框: 记不清文本框: 不知道（名），

    估计这所学校有1500名学生知道母亲的生日．??????????????????????????????????????????????????? （6分）

    （3）略（语言表述积极进取，健康向上即可得分）．?????????????????????????????????????????????? （7分）

    ２１．(本题满分８分)

    解：（1）如图，由题意得，∠EAD=45°，∠FBD=30°．

    ∴ ∠EAC=∠EAD+∠DAC =45°+15°=60°．

    ∵  AE∥BF∥CD，

    ∴  ∠FBC=∠EAC=60°．

    ∴ ∠DBC=30°．　???????????????????????????????????????? 2分

    又∵ ∠DBC=∠DAB+∠ADB，

    　　∴ ∠ADB=15°．

    ∴ ∠DAB=∠ADB． ∴  BD=AB=2．

    　　即B，D之间的距离为2km．???????????????????????????????????????????????????????????????????????????????? ４分

    （2）过B作BO⊥DC，交其延长线于点O，

    　　在Rt△DBO中，BD=2，∠DBO=60°．

    　　∴ DO=2×sin60°=2×,BO=2×cos60°=1．??????????????????????????????????????????????????? ６分

    　　在Rt△CBO中，∠CBO=30°，CO=BOtan30°=，

    　　∴ CD=DO－CO=（km）．

    　　即C，D之间的距离为km． ????????????????????????????????????????????????????????????????????????? ８分

     

    ２２．解：（1）

    （2）290，甲，20．????????????????????????????????????????????????????????????????????????????????? 6分（每空1分）

    （3）在5月17日，甲厂生产帐篷50顶，乙厂生产帐篷30顶．???????????????????????????????????? 6分

    设乙厂每天生产帐篷的数量提高了，则?????????????????????????????????????? 7分

    ．

    答：乙厂每天生产帐篷的数量提高了．?????????????????????????????????????????????????????????????????? 8分

     

     

    ２３．解：（1）① 等边三角形；②重叠三角形的面积为．?????????????????????????? 5分

    （2）用含的代数式表示重叠三角形的面积为；?????????????????????????? 7分

    的取值范围为．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．8分

    （3）能；t=2。．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．１０分．

    ２４．本小题满分1０分．

    （Ⅰ）证明  将△沿直线对折，得△，连，

    则△≌△．    ????????????????????????????????????????????????????????????????????????????????????????? 1分

    有，，，．

    又由，得 ．  ????????????????????????????????????????? 2分

    由，

    ，

    得． ??????????????????????????????????????????????????????????????????????????????????????????????????? 3分

    又，

    ∴△≌△．    ???????????????????????????????????????????????????????????????????????????????????????????? 4分

    有，．

    ∴．???????????????????????????????????????????????????????????? ５分

    ∴在Rt△中，由勾股定理，

    得．即． ??????????????????????????????????????????????????????? ６分

    （Ⅱ）关系式仍然成立．  ???????????????????????????????????????????????????????????? ７分

    证明  将△沿直线对折，得△，连，

    则△≌△． ???????????????????????????????????????????????????? 8分

    有，，

    ，．

    又由，得 ．

    由，

    ．

    得．   ??????????????????????????????????????????????????????????????????????????????????????????????? ８分

    又，

    ∴△≌△．

    有，，，

    ∴．  

    ∴在Rt△中，由勾股定理，

    得．即．????????????????????????????????????????????????????????? ９分

    （３）．能；在直线ＡＢ上取点Ｍ，Ｎ使∠ＭＣＮ＝４５°．．．．．．．．．．．．．．．．．．．．．．１０分

    ２５．（本题满分12分）

    解：（1）设正方形的边长为cm，则

    ．?????????????????????????????????????????????????????????????????????????????????????????????? 1分

    即．

    解得（不合题意，舍去），．

    剪去的正方形的边长为1cm．???????????????????????????????????????????????????????????????????????????????????? 3分

    （注：通过观察、验证直接写出正确结果给3分）

    （2）有侧面积最大的情况．

    设正方形的边长为cm，盒子的侧面积为cm2，

    则与的函数关系式为：

    ．

    即．????????????????????????????????????????????????????????????????????????????????????????????????????? 5分

    改写为．

    当时，．

    即当剪去的正方形的边长为2.25cm时，长方体盒子的侧面积最大为40.5cm2．?????????????? 7分

    （3）有侧面积最大的情况．

    设正方形的边长为cm，盒子的侧面积为cm2．

    若按图1所示的方法剪折，则与的函数关系式为：

    ．

    即．

    当时，．??????????????????????????????????? 9分

    若按图2所示的方法剪折，则与的函数关系式为：

    ．

    即．

    当时，．??????????????????????????????????????????????????????????????????????????????????????? 11分

    比较以上两种剪折方法可以看出，按图2所示的方法剪折得到的盒子侧面积最大，即当剪去的正方形的边长为cm时，折成的有盖长方体盒子的侧面积最大，最大面积为cm2．

    说明：解答题各小题只给了一种解答及评分说明，其他解法只要步骤合理，解答正确，均应给出相应分数．

    ２６．（本小题满分12分）

    解：（1）在Rt△ABC中，，

    由题意知：AP = 5－t，AQ = 2t，

    若PQ∥BC，则△APQ ∽△ABC，

    ∴，

    ∴，

    ∴．                                 ??????????????????????????????????????????????????????? 3′

    （2）过点P作PH⊥AC于H．

    ∵△APH ∽△ABC，

    ∴，

    ∴，

    ∴，

    ∴．    　  ??????????????????????????????????????????? 6′

    （3）若PQ把△ABC周长平分，

    则AP+AQ=BP+BC+CQ．

    ∴，   

    解得：．

    若PQ把△ABC面积平分，

    则，  即－＋3t=3．

    ∵ t=1代入上面方程不成立，

    ∴不存在这一时刻t，使线段PQ把Rt△ACB的周长和面积同时平分．???????????????? 9′

    （4）过点P作PM⊥AC于Ｍ，PN⊥BC于N，

    若四边形PQP ′ C是菱形，那么PQ＝PC．

    ∵PM⊥AC于M，

    ∴QM=CM．

    ∵PN⊥BC于N，易知△PBN∽△ABC．

    ∴，  ∴，

    ∴，

    ∴，

    ∴，

    解得：．

    ∴当时，四边形PQP ′ C 是菱形．     

    此时，　，

    在Rt△PMC中，，

    ∴菱形PQP ′ C边长为．?????????????????????????????????????????????????????????????????????????? 12′

     

     

     

     


    同步练习册答案