
题目列表(包括答案和解析)
解析:依题意得f(x)的图象关于直线x=1对称,f(x+1)=-f(x-1),f(x+2)=-f(x),f(x+4)=-f(x+2)=f(x),即函数f(x)是以4为周期的函数.由f(x)在[3,5]上是增函数与f(x)的图象关于直线x=1对称得,f(x)在[-3,-1]上是减函数.又函数f(x)是以4为周期的函数,因此f(x)在[1,3]上是减函数,f(x)在[1,3]上的最大值是f(1),最小值是f(3).
答案:A
| ||
| 2 |
| ||
| 3 |
| ||
| 3 |
| ||
| 2 |
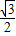 倍”,请你写出此命题在立体几何中类似的真命题:______
倍”,请你写出此命题在立体几何中类似的真命题:______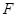 是抛物线
是抛物线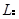
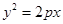
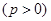 的焦点,
的焦点,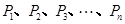 是抛物线
是抛物线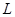 上的
上的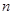 个不同的点(
个不同的点(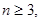
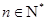 ).
).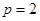 时,试写出抛物线
时,试写出抛物线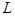 上的三个定点
上的三个定点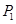 、
、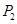 、
、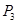 的坐标,从而使得
的坐标,从而使得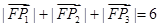 ;
;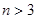 时,若
时,若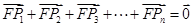 ,
, ;
;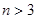 时,某同学对(2)的逆命题,即:
时,某同学对(2)的逆命题,即: ,则
,则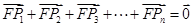 .”
.”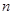 ,试构造该假命题反例的一般形式,并说明你的理由(本研究方向最高得8分);
,试构造该假命题反例的一般形式,并说明你的理由(本研究方向最高得8分);湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com