练习册

  • 练习册
  • 试题
    18． 【查看更多】

     

    题目列表(包括答案和解析)

    (本小题满分12分)

       如图，在平面直角坐标系中，△ABC的A、B两个顶点在x轴上，顶点C在y轴的负半轴上．已知，，△ABC的面积，抛物线

    经过A、B、C三点。

       1.(1)求此抛物线的函数表达式；

       2.(2)设E是y轴右侧抛物线上异于点B的一个动点，过点E作x轴的平行线交抛物线于另一点F，过点F作FG垂直于x轴于点G，再过点E作EH垂直于x轴于点H，得到矩形EFGH．则在点E的运动过程中，当矩形EFGH为正方形时，求出该正方形的边长；

       3.(3)在抛物线上是否存在异于B、C的点M，使△MBC中BC边上的高为？若存在，求出点M的坐标；若不存在，请说明理由．

     

    查看答案和解析>>

    (本小题满分8分)

       某学校要在围墙旁建一个长方形的中药材种植实习苗圃，苗圃的一边靠围墙(墙的长度不限)，另三边用木栏围成，建成的苗圃为如图所示的长方形ABCD。已知木栏总长为120米，设AB边的长为x米，长方形ABCD的面积为S平方米．

       1.(1)求S与x之间的函数关系式(不要求写出自变量x的取值范围)．当x为何值时，S取得最值(请指出是最大值还是最小值)?并求出这个最值；

       2.(2)学校计划将苗圃内药材种植区域设计为如图所示的两个相外切的等圆，其圆心分别为和，且到AB、BC、AD的距离与到CD、BC、AD的距离都相等，并要求在苗圃内药材种植区域外四周至少要留够0.5米宽的平直路面，以方便同学们参观学习．当(l)中S取得最值时，请问这个设计是否可行?若可行，求出圆的半径；若不可行，清说明理由．

     

    查看答案和解析>>

    (本小题满分1 0分)

    如图，已知线段AB∥CD，AD与B C相交于点K，E是线段AD上一动点。

       1.(1)若BK=KC，求的值；

    2.(2)连接BE，若BE平分∠ABC，则当AE= AD时，猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明．再探究：当AE=AD(n>2)，而其余条件不变时，线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论，不必证明．

     

    查看答案和解析>>

    (本小题满分1 0分)

    如图，已知反比例函数的图象经过点(，8)，直线经过该反比例函数图象上的点Q(4，m)．

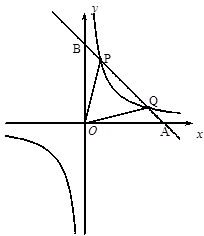
       1.(1)求上述反比例函数和直线的函数表达式；

       2.(2)设该直线与x轴、y轴分别相交于A 、B两点，与反比例函数图象的另一个交点为P，连结0P、OQ，求△OPQ的面积．

     

    查看答案和解析>>

    (本小题满分8分)

        某市今年的信息技术结业考试，采用学生抽签的方式决定自己的考试内容。规定：每位考生先在三个笔试题（题签分别用代码表示）中抽取一个，再在三个上机题（题签分别用代码表示）中抽取一个进行考试。小亮在看不到题签的情况下，分别从笔试题和上机题中随机地各抽取一个题签。

    1.（1）用树状图或列表法表示出所有可能的结构；

    2.（2）求小亮抽到的笔试题和上机题的题签代码的下标（例如“”的下表为“1”）均为奇数的概率。

     

    查看答案和解析>>

    一、选择题

    1．A　2．B　3．C　4．B　5．B　6．C　7．C　8．A　9．B　10．D　11．B　12．C

    二、填空题

    13．9　　14．　　15． BD=CD，OE=OF，DE∥AC等　　16．4　　17．15

    三、解答题

    18．

    （1）解：   ................................................ 1分

       ...................................................... 2分

      ....................................................... 3分

    （2）解：解①得＞－2  ................................................ 4分

    解②得＜3  .................................................. 5分

    ∴此不等式组的解集是－2＜x＜3    ................................... 6分

    解集在数轴上表示正确  .............................................. 7分

    19．

    （1）证明：∵AB∥DE，∴∠B=∠DEF

    ∵AC∥DF，∴∠F=∠ACB  ............................................ 1分

    ∵BE=CF，∴BE+EC= CF + EC即BC=EF   ............................... 2分

    ∴△ABC≌△DEF

    ∴AB=DE............................. 3分

    （2）解：过点O作OG⊥AP于点G

    连接OF  ........................... 4分

    ∵ DB=10，∴ OD=5

    ∴ AO=AD+OD=3+5=8

    ∵∠PAC=30°

    ∴ OG=AO=cm............... 5分

    ∵ OG⊥EF，∴ EG=GF

    ∵ GF= 

    ∴ EF=6cm  ......................... 7分

    20．解：组成的所有坐标列树状图为：

     

    .................... 5分

    或列表为：

    .................... 5分

    方法一：根据已知的数据，点不在第二象限的概率为

    方法二：1－  ................................................. 8分

    21．解：设康乃馨每支元，水仙花每支元   ............................. 1分

    由题意得：    ......................................... 4分

    解得：  ..................................................... 6分

    第三束花的价格为  ................................ 7分

    答：第三束花的价格是17元．   ...................................... 8分

    22．解:（1）设CD为千米，

    由题意得，∠CBD=30°，∠CAD=45°

    ∴AD=CD=x  .................... 1分

    在Rt△BCD中，tan30°=

    ∴ BD=  ................... 2分

    AD+DB=AB=40

    ∴   ............... 3分

    解得 ≈14.7

    ∴ 牧民区到公路的最短距离CD为14.7千米．  ......................... 4分

    （若用分母有理化得到CD=14.6千米，可得4分）

    （2）设汽车在草地上行驶的速度为，则在公路上行驶的速度为3，

    在Rt△ADC中，∠CAD=45°，∴ AC=CD

    方案I用的时间........................ 5分

    方案II用的时间..................................... 6分

    ∴

    = .................................................... 7分

    ∵ ＞0

    ∴ ＞0  ...................................................... 8分

    ∴方案I用的时间少，方案I比较合理  ............................... 9分

    23．解：（1）  .......................................... 1分

    解得：   .................................................. 2分

    ∴点P的坐标为(2，)  ........................................... 3分

    （2）将代入

    ∴ ，即OA=4................................................... 4分

    做PD⊥OA于D，则OD=2，PD=2

    ∵ tan∠POA=

    ∴ ∠POA=60°   ................................................... 5分

    ∵ OP=

    ∴△POA是等边三角形．  ............ 6分

     

    （3）① 当0<t≤4时，如图1

    在Rt△EOF中，∵∠EOF=60°，OE=t

    ∴EF=t，OF=t

    ∴S=?OF?EF=.............. 7分

    当4<t<8时，如图2

    设EB与OP相交于点C

    易知：CE=PE=t－4，AE=8－t

    ∴AF=4－，EF=(8－t)  

    ∴OF=OA－AF=4－（4－t）=t

    ∴S=(CE+OF)?EF

    =(t－4+t)×(8－t）

    =－+4t－8................ 8分

    ② 当0<t≤4时，S=， t=4时，S最大=2

    当4<t<8时，S=－+4t－8=－(t－)+ 

    t=时，S最大=

    ∵>2，∴当t=时，S最大=........................... 9分

    24．解：(1)设抛物线的解析式为  ......................... 1分

    将A(－1，0)代入:       ∴   .................... 2分

    ∴ 抛物线的解析式为，即：.............. 3分

    （2）是定值，  ........................................... 4分

    ∵ AB为直径，∴ ∠AEB=90°，∵ PM⊥AE，∴ PM∥BE

    ∴ △APM∽△ABE，∴  ①

    同理:   ②  .............................................. 5分

    ① + ②: .................................... 6分

    （3）∵ 直线EC为抛物线对称轴，∴ EC垂直平分AB

    ∴ EA=EB

    ∵ ∠AEB=90°

    ∴ △AEB为等腰直角三角形．

    ∴ ∠EAB=∠EBA=45° ........... 7分

    如图，过点P作PH⊥BE于H，

    由已知及作法可知，四边形PHEM是矩形，

    ∴PH=ME且PH∥ME

    在△APM和△PBH中

    ∵∠AMP=∠PHB=90°， ∠EAB=∠BPH=45°

    ∴ PH=BH

    且△APM∽△PBH

    ∴

    ∴ 　①.......... 8分

    在△MEP和△EGF中，

    ∵ PE⊥FG，  ∴ ∠FGE+∠SEG=90°

    ∵∠MEP+∠SEG=90°  ∴ ∠FGE=∠MEP

    ∵ ∠PME=∠FEG=90° ∴△MEP∽△EGF

    ∴ 　　　　②

    由①、②知：.............................................. 9分

    （本题若按分类证明，只要合理，可给满分）

     

     

     

     

     


    同步练习册答案