题目列表(包括答案和解析)
调查班里同学的人际关系．
一、设计 调查问卷
问卷编号：________年________月________日
调查目的 了解班里同学的人际关系
调查对象 性别 年龄 职业
调查内容
(1)你能背出几个本班同学家的电话号码吗？ ( )
A．多于7个 B．4～7个 C．0～3个
(2)你在本班的朋友多，还是外班的朋友多？ ( )
A．本班的多 B．一样多 C．外班的多
(3)在班里，你是“小领袖”，还是“小随从”？ ( )
A．我没考虑过 B．大多数人听我的话 C．多数情况下我听别人的
(4)你觉得可不可以向老师打小报告？ ( )
A．不行 B．最好不要 C．当然可以
(5)如果朋友搞你的恶作剧，你会怎么样？ ( )
A．和他们一起笑
B．看自己心情如何，也许和他们一起大笑，也许生气发怒
C．生气发怒
(6)当你的同学有困难时，他们是否愿意求得你的帮助？ ( )
A．非常愿意 B．只有关系密切的同学才来求助 C．不愿意
(7)当朋友向你吐露了一个极有趣的个人问题后，你会怎么样？ ( )
A．没有考虑是否要把这件事报告别人
B．努力保守秘密
C．在朋友离开后不久，便找个第三者参与评论
二、实施调查
三、处理数据
以选择A得3分、B、得2分、C得0分计算整理．21～15分的人在班里受大家欢迎，和大家相处很好；15～5分的人有自己的朋友圈子，但很少关心圈外的人；4～0分的人在班里朋友很少．
四、交流
发现班里同学人际关系好的要多关心帮助那些孤独的人，并提醒那些在班里朋友很少的人要多关心他人，不要只想着自己，要多参加集体活动．
五、写一份调查报告．
如果a,b互为相反数，x,y互为倒数，则
的值是（ ）
A．2 B. 3 C. 3.5 D. 4
10、点C在线段AB上，下列条件中不能确定点C是线段AB中点的是（ ）
A．AC=BC B．AC + BC= AB C．AB =2AC D．BC =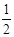
AB
| 得分 | 评卷人 |
|
|
|
如果a,b互为相反数，x,y互为倒数，则
的值是（ ）
A．2 B. 3 C. 3.5 D. 4
10、点C在线段AB上，下列条件中不能确定点C是线段AB中点的是（ ）
A．AC
=BC B．AC + BC= AB C．AB =2AC D．BC =
AB
|
得分 |
评卷人 |
|
|
|
一、选择题
1．A 2．B 3．C 4．B 5．B 6．C 7．C 8．A 9．B 10．D 11．B 12．C
二、填空题
13．9 14．
15． BD=CD，OE=OF，DE∥AC等 16．4 17．15
三、解答题
18．
（1）解：
................................................ 1分
...................................................... 2分
....................................................... 3分
（2）解：解①得
＞－2 ................................................ 4分
解②得＜3 .................................................. 5分
∴此不等式组的解集是－2＜x＜3 ................................... 6分
解集在数轴上表示正确 .............................................. 7分
19．
（1）证明：∵AB∥DE，∴∠B=∠DEF
∵AC∥DF，∴∠F=∠ACB ............................................ 1分
∵BE=CF，∴BE+EC= CF + EC即BC=EF ............................... 2分
∴△ABC≌△DEF
∴AB=DE............................. 3分
（2）解：过点O作OG⊥AP于点G
连接OF ........................... 4分
∵ DB=10，∴ OD=5
∴ AO=AD+OD=3+5=8
∵∠PAC=30°
∴ OG=
AO=
cm............... 5分
∵ OG⊥EF，∴ EG=GF
∵ GF=
∴ EF=
20．解：组成的所有坐标列树状图为：
.................... 5分
或列表为：
.................... 5分
方法一：根据已知的数据，点
不在第二象限的概率为
方法二：1－
................................................. 8分
21．解：设康乃馨每支元，水仙花每支
元 ............................. 1分
由题意得：
......................................... 4分
解得：
..................................................... 6分
第三束花的价格为
................................ 7分
答：第三束花的价格是17元． ...................................... 8分
22．解:（1）设CD为千米，
由题意得，∠CBD=30°，∠CAD=45°
∴AD=CD=x .................... 1分
在Rt△BCD中，tan30°=
∴ BD=
................... 2分
AD+DB=AB=40
∴ 
............... 3分
解得 ≈14.7
∴ 牧民区到公路的最短距离CD为14.7千米． ......................... 4分
（若用分母有理化得到CD=
（2）设汽车在草地上行驶的速度为
，则在公路上行驶的速度为3，
在Rt△ADC中，∠CAD=45°，∴ AC=
CD
方案I用的时间
........................ 5分
方案II用的时间
..................................... 6分
∴ 
=
.................................................... 7分
∵ 
＞0
∴ 
＞0 ...................................................... 8分
∴方案I用的时间少，方案I比较合理 ............................... 9分
23．解：（1）
.......................................... 1分
解得：
.................................................. 2分
∴点P的坐标为(2，
) ........................................... 3分
（2）将
代入
∴ 
，即OA=4................................................... 4分
做PD⊥OA于D，则OD=2，PD=2
∵ tan∠POA=
∴ ∠POA=60° ................................................... 5分
∵ OP=
∴△POA是等边三角形． ............ 6分
（3）① 当0<t≤4时，如图1
在Rt△EOF中，∵∠EOF=60°，OE=t
∴EF=
t，OF=
t
∴S=?OF?EF=
.............. 7分
当4<t<8时，如图2
设EB与OP相交于点C
易知：CE=PE=t－4，AE=8－t
∴AF=4－
，EF=(8－t)
∴OF=OA－AF=4－（4－t）=t
∴S=(CE+OF)?EF
=
(t－4+t)×
(8－t）
=－
+4
t－8................ 8分
② 当0<t≤4时，S=
， t=4时，S最大=2
当4<t<8时，S=－+4t－8=－(t－
)
+
t=时，S最大=
∵>2，∴当t=时，S最大=........................... 9分
24．解：(1)设抛物线的解析式为
......................... 1分
将A(－1，0)代入: 
∴ 
.................... 2分
∴ 抛物线的解析式为
，即：
.............. 3分
（2）是定值，
........................................... 4分
∵ AB为直径，∴ ∠AEB=90°，∵ PM⊥AE，∴ PM∥BE
∴ △APM∽△ABE，∴ 
①
同理: 
② .............................................. 5分
① + ②:
.................................... 6分
（3）∵ 直线EC为抛物线对称轴，∴ EC垂直平分AB
∴ EA=EB
∵ ∠AEB=90°
∴ △AEB为等腰直角三角形．
∴ ∠EAB=∠EBA=45° ........... 7分
如图，过点P作PH⊥BE于H，
由已知及作法可知，四边形PHEM是矩形，
∴PH=ME且PH∥ME
在△APM和△PBH中
∵∠AMP=∠PHB=90°， ∠EAB=∠BPH=45°
∴ PH=BH
且△APM∽△PBH
∴ 
∴ 
①.......... 8分
在△MEP和△EGF中，
∵ PE⊥FG， ∴ ∠FGE+∠SEG=90°
∵∠MEP+∠SEG=90° ∴ ∠FGE=∠MEP
∵ ∠PME=∠FEG=90° ∴△MEP∽△EGF
∴
②
由①、②知：
.............................................. 9分
（本题若按分类证明，只要合理，可给满分）
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com