
题目列表(包括答案和解析)
(本小题满分12分)已知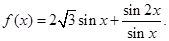
(I)求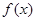 的最大值,及当取最大值时x的取值集合。
的最大值,及当取最大值时x的取值集合。
(II)在三角形ABC中a、b、c分别是角A、B、C所对的边,对定义域内任意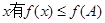 ,且b=1,c=2,求a的值。
,且b=1,c=2,求a的值。
(本小题满分12分)已知
(I)求 的最大值,及当取最大值时x的取值集合。
的最大值,及当取最大值时x的取值集合。
(II)在三角形ABC中a、b、c分别是角A、B、C所对的边,对定义域内任意 ,且b=1,c=2,求a的值。
,且b=1,c=2,求a的值。
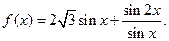
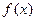 的最大值,及当取最大值时x的取值集合。
的最大值,及当取最大值时x的取值集合。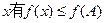 ,且b=1,c=2,求a的值。
,且b=1,c=2,求a的值。己知在锐角ΔABC中,角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]()
(I )求角![]() 大小;
大小;
(II)当![]() 时,求
时,求![]() 的取值范围.
的取值范围.

20.如图1,在平面内,![]() 是
是![]() 的矩形,
的矩形,![]() 是正三角形,将
是正三角形,将![]() 沿
沿![]() 折起,使
折起,使![]() 如图2,
如图2,![]() 为
为![]() 的中点,设直线
的中点,设直线![]() 过点
过点![]() 且垂直于矩形
且垂直于矩形![]() 所在平面,点
所在平面,点![]() 是直线
是直线![]() 上的一个动点,且与点
上的一个动点,且与点![]() 位于平面
位于平面![]() 的同侧。
的同侧。
(1)求证:![]() 平面
平面![]() ;
;
(2)设二面角![]() 的平面角为
的平面角为![]() ,若
,若![]() ,求线段
,求线段![]() 长的取值范围。
长的取值范围。


21.已知A,B是椭圆![]() 的左,右顶点,
的左,右顶点,![]() ,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线
,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线![]() 于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
(1)求椭圆C的方程;
 (2)求三角形MNT的面积的最大值
(2)求三角形MNT的面积的最大值
22. 已知函数![]()
![]() ,
,
(Ⅰ)若![]() 在
在![]() 上存在最大值与最小值,且其最大值与最小值的和为
上存在最大值与最小值,且其最大值与最小值的和为![]() ,试求
,试求![]() 和
和![]() 的值。
的值。
(Ⅱ)若![]() 为奇函数:
为奇函数:
(1)是否存在实数![]() ,使得
,使得![]() 在
在![]() 为增函数,
为增函数,![]() 为减函数,若存在,求出
为减函数,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(2)如果当![]() 时,都有
时,都有![]() 恒成立,试求
恒成立,试求![]() 的取值范围.
的取值范围.
已知锐角![]() 中,
中,![]() 三个内角为A、B、C,两向量
三个内角为A、B、C,两向量![]() ,
,![]() 。若
。若![]() 与
与![]() 是共线向量.
是共线向量.
(I)求![]() 的大小;
的大小;
(II)求函数![]() 取最大值时,
取最大值时,![]() 的大小.
的大小.
一、选择题
CBACB DBADC AC
二、填空题
13..files/image264.gif) 14.
14..files/image266.gif) 15.
15..files/image020.gif) 16.
16..files/image137.gif)
三、解答题
17.解:(I).files/image270.gif)
( II ) .files/image272.gif)
18解:(I)依题意,记“甲投一次命中”为事件A,“乙投一次命中”为事件B,
即p(A)=.files/image016.gif) ,p(B)=
,p(B)=.files/image275.gif) , 甲乙两人在罚球线各投球一次两人得分之和
, 甲乙两人在罚球线各投球一次两人得分之和.files/image204.gif) 的可能取值为0,1,2,则
的可能取值为0,1,2,则.files/image204.gif)
的概率分布为:
.files/image204.gif)
0
1
2
p
.files/image277.gif)
.files/image016.gif)
.files/image280.gif)
.files/image282.gif)
( II ).files/image284.gif) 事件“甲乙两人在罚球线各投球二次均不命中”的概率为
事件“甲乙两人在罚球线各投球二次均不命中”的概率为.files/image286.gif)
.files/image288.gif) 甲乙两人在罚球线各投球两次,这四次投球中至少一次命中的概率为p=
甲乙两人在罚球线各投球两次,这四次投球中至少一次命中的概率为p=.files/image290.gif)
19解:(I)证明:.files/image284.gif) ABCD为正方形
ABCD为正方形.files/image293.gif)
.files/image295.gif)
.files/image297.gif)
故.files/image299.gif)
.files/image288.gif) 平面
平面.files/image213.gif) 平面
平面.files/image210.gif)
( II )联结.files/image302.gif)
.files/image304.gif) ,
,
.files/image306.gif)
用等体积法.files/image308.gif) ,得所求距离为
,得所求距离为.files/image034.gif)
(III)在平面中.files/image311.gif) ,过点O作
,过点O作.files/image313.gif) 于点F,联结DF,易证
于点F,联结DF,易证.files/image315.gif) 就是所求二面角的平面角,
就是所求二面角的平面角,
设.files/image222.gif) 为a,在
为a,在.files/image318.gif) 中,
中,.files/image320.gif)
.files/image322.gif)
20解:(I)易得.files/image324.gif) 。
。
当.files/image326.gif) ,
,
.files/image328.gif)
.files/image330.gif)
( II ).files/image332.gif)
.files/image334.gif)
.files/image336.gif)
.files/image338.gif)
21解:(I)设P(x,y),.files/image340.gif)
.files/image342.gif)
.files/image344.gif)
.files/image346.gif)
( II )设.files/image348.gif) ,联立
,联立.files/image350.gif) 得
得.files/image352.gif)
.files/image354.gif)
则.files/image356.gif)
又.files/image358.gif)
∵以MN为直径的圆过右顶点A
∴.files/image360.gif)
∴.files/image362.gif)
∴.files/image364.gif)
化简整理得.files/image366.gif)
∴.files/image368.gif) ,且均满足
,且均满足.files/image370.gif)
当.files/image372.gif) 时,直线
时,直线.files/image252.gif) 的方程为
的方程为.files/image375.gif) ,直线过定点(2,0),与已知矛盾!
,直线过定点(2,0),与已知矛盾!
当.files/image377.gif) 时,直线
时,直线.files/image252.gif) 的方程为
的方程为.files/image379.gif) ,直线过定点(
,直线过定点(.files/image381.gif) ,0)
,0)
∴直线.files/image252.gif) 定点,定点坐标为(
定点,定点坐标为(.files/image381.gif) ,0)。
,0)。
22解:(I).files/image384.gif)
( II ).files/image386.gif)
若x=0,.files/image388.gif) 显然成立;
显然成立;
当.files/image390.gif)
.files/image392.gif)
.files/image394.gif)
显然x=1是函数.files/image396.gif) 的极(最)小值点,
的极(最)小值点,.files/image398.gif)
.files/image400.gif)
(III)由(1)得,对任意.files/image402.gif) ,恒有
,恒有.files/image404.gif)
.files/image406.gif)
.files/image408.gif)
.files/image410.gif)
即.files/image262.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com