
题目列表(包括答案和解析)
(本小题满分12分)现有一张长为40dm,宽为20dm的长方形铁皮,准备通过分割、焊接成一个无盖的长方体水箱(损耗忽略不计)。 (1)若从长方形的四个角各截去一个边长为![]() dm的小正方形,再把四边向上翻转
dm的小正方形,再把四边向上翻转![]() 角,焊接成一个无盖的长方体水箱,求:水箱容积的最大值。(2)设(1)中水箱容积的最大值为M,你是否还有其它的设计方案,使你的设计中得到的长方体水箱的容积比M还大?若有,写出你的设计方案,并求出它的容积;若没有,请说明理由。
角,焊接成一个无盖的长方体水箱,求:水箱容积的最大值。(2)设(1)中水箱容积的最大值为M,你是否还有其它的设计方案,使你的设计中得到的长方体水箱的容积比M还大?若有,写出你的设计方案,并求出它的容积;若没有,请说明理由。
(本小题满分12分)已知各项均为正数的数列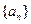 中,
中,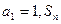 是数列
是数列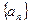 的前
的前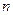 项和,对任意
项和,对任意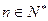 ,有
,有 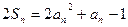 .函数
.函数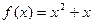 ,数列
,数列 的首项
的首项 .
.
(Ⅰ)求数列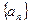 的通项公式;
的通项公式;
(Ⅱ)令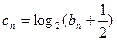 求证:
求证: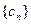 是等比数列并求
是等比数列并求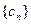 通项公式;
通项公式;
(Ⅲ)令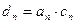 ,
, ,求数列
,求数列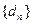 的前n项和
的前n项和 .
.
(本小题满分12分)
已知各项均为正数的数列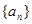 的前n项和
的前n项和 满足
满足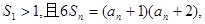
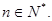
(1)求数列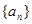 的通项公式;
的通项公式;
(2)设数列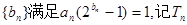 为数列
为数列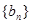 的前n项和,求证:
的前n项和,求证:
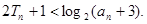
(本小题满分12分)
已知 是公差为正数的等差数列,首项
是公差为正数的等差数列,首项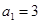 ,前n项和为Sn,数列
,前n项和为Sn,数列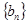 是等比数列,首项
是等比数列,首项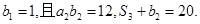
(1)求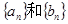 的通项公式.
的通项公式.
(2)令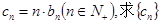 的前n项和Tn.
的前n项和Tn.
(本小题满分12分)已知各项均为正数的数列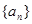 的前
的前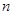 项和
项和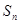 满足
满足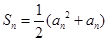
(1)求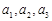 的值; (2)求
的值; (2)求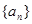 的通项公式;
的通项公式;
(3)是否存在正数 使下列不等式:
使下列不等式:

对一切 成立?若存在,求出M的取值范围;若不存在,请说明理由
成立?若存在,求出M的取值范围;若不存在,请说明理由
一、选择题.(单项选择,5×12=60分.答案涂在答题卡上的相应位置.)
1.C 2. A 3. B 4. B 5. B 6. B 7. A 8. C 9.D 10. B 11.D 12. B
二、填空题.( 5×4=20分,答案写在答题纸的相应空格内.)
|