练习册

  • 练习册
  • 试题
    (Ⅰ)两数之和小于1.2, 【查看更多】

     

    题目列表(包括答案和解析)

    （本小题满分12分）

        东莞市政府要用三辆汽车从新市政府把工作人员接到老市政府，已知从新市政府到老市政府有两条公路，汽车走公路①堵车的概率为，不堵车的概率为；汽车走公路②堵车的概率为，不堵车的概率为．若甲、乙两辆汽车走公路①，丙汽车由于其他原因走公路②，且三辆车是否堵车相互之间没有影响．

       （1）若三辆汽车中恰有一辆汽车被堵的概率为，求走公路②堵车的概率；

       （2）在（1）的条件下，求三辆汽车中被堵车辆的个数的分布列和数学期望．

    查看答案和解析>>

    （本小题满分12分）
    商店出售茶壶和茶杯，茶壶单价为每个20元，茶杯单价为每个5元，该店推出两种促销优惠办法：
    （1）买1个茶壶赠送1个茶杯；
    （2）按总价打9折付款（即按原价的90%付款）。
    某顾客需要购买茶壶4个，茶杯若干个，（不少于4个），若以购买茶杯数为x个，付款数为y（元），试分别建立两种优惠办法中y与x之间的函数关系式，并讨论该顾客买同样多的茶杯时，两种办法哪一种更省钱？

    查看答案和解析>>

    （本题满分15分）某地建一座桥，两端的桥墩已建好，这两墩相距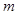米，余下工程只需要建两端桥墩之间的桥面和桥墩，经预测，建一个桥墩的工程费用为256万元，距离为米的相邻两桥墩之间的桥面工程费用为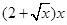万元。假设桥墩等距离分布，所有桥墩都视为点，且不考虑其他因素，记余下工程的费用为万元。

    （1）试写出关于的函数关系式； 

    （2）当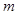=640米时，需新建多少个桥墩才能使最小？

     

    查看答案和解析>>

    （本小题满分12分）

        东莞市政府要用三辆汽车从新市政府把工作人员接到老市政府，已知从新市政府到老市政府有两条公路，汽车走公路①堵车的概率为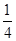，不堵车的概率为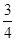；汽车走公路②堵车的概率为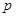，不堵车的概率为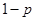．若甲、乙两辆汽车走公路①，丙汽车由于其他原因走公路②，且三辆车是否堵车相互之间没有影响．

    （1）若三辆汽车中恰有一辆汽车被堵的概率为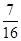，求走公路②堵车的概率；

    （2）在（1）的条件下，求三辆汽车中被堵车辆的个数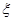的分布列和数学期望．

     

    查看答案和解析>>

    （本小题满分12分）

    从某学校高三年级共800名男生中随机抽取50名测量身高，测量发现被测学生身高全部介于155 cm 和195 cm之间，将测量结果按如下方式分成八组：第一组[155,160)、第二组[160,165)、…、第八组[190,195]，下图是按上述分组方法得到的频率分布直方图的一部分，已知第一组与第八组人数相同，第六组、第七组、第八组人数依次构成等差数列．

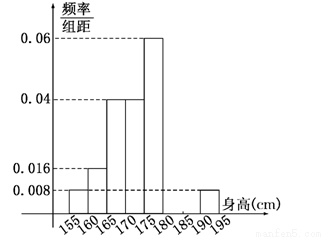
    (1)估计这所学校高三年级全体男生身高180 cm以上(含180 cm)的人数；

    (2)求第六组、第七组的频率并补充完整频率分布直方图；

    (3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生，记他们的身高分别为x、y，求满足|x－y|≤5的事件概率．

     

    查看答案和解析>>

    一、选择题：每小题5分，满分60分.

    题号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    答案

    B

    C

    A

    A

    A

    A

    B

    D

    D

    B

    C

    C

    二、填空题：每小题5分，满分20分.

    13．

    14．　

    15．

    16．①③④

    三、解答题

    17．设两个实数为a，b，，，建立平面直角坐标系aOb， 则点在正方形OABC内       ……… 2分

    (Ⅰ) 记事件A“两数之和小于1.2”，即，则满足条件的点在多边形OAEFC内

    所以                                    ……… 6分

    (Ⅱ) 记事件B“两数的平方和小于0.25”，则满足条件的点在扇形内

    所以                                                                    ………10分

    18．∵m?n ∴                                ……… 4分

    　　再由余弦定理得：

    （Ⅰ）由得，故                      ……… 8分

    （Ⅱ）由得

    解得，所以的取值范围是         ………12分

    19．（Ⅰ）连接，交于，易知为、中点，故在△中，为边的中位线，故∥，平面，平面，所以∥平面            ……… 5分

    （Ⅱ）在平面内过点作⊥，垂足为H，

    ∵平面⊥平面，且平面∩平面，

    ∴⊥平面，∴⊥，                                 ……… 8分

    又∵，为中点，∴⊥

    ∴⊥平面，∴⊥，又∵，

    ∴⊥平面．                                                           ………12分

    20．（Ⅰ）∵是各项均为正数的等差数列，且公差

    ∴　∴           ……… 3分

    ∴为常数，∴是等差数列           ……… 5分

    （Ⅱ）∵，∴

    ∴是公差为1的等差数列                                       ……… 7分

    ∴，∴       ……… 9分

    当时，                                   ………10分

    当时，

    综上，                                                               ………12分

    21．（Ⅰ）                                                                       ……… 4分

    （Ⅱ）由椭圆的对称性知：PRQS为菱形，原点O到各边距离相等……… 5分

    ⑴当P在y轴上时，易知R在x轴上，此时PR方程为，

    ．                                                       ……… 6分

    ⑵当P在x轴上时，易知R在y轴上，此时PR方程为，

    ．                                                       ……… 7分

    ⑶当P不在坐标轴上时，设PQ斜率为k，、

    P在椭圆上，.......①；R在椭圆上，......②

    利用Rt△POR可得　                              ……… 9分

    即　

    整理得　．                                               ………11分

    再将①②带入，得

    综上当时，有．                                       ………12分

    22．（Ⅰ）∵，且，∴

    ∴在上， 和变化情况如下表：

    x

    ０

    １

     

    ＋

    ０

    －

     

    ↑

    b

    ↓

                                                                                                ……… 2分

    ∵函数在上的最大值为1，

    ∴，此时应有 ∴

    ∴，                                                                  ……… 4分

    （Ⅱ）                                                                             ……… 6分

    所求切线方程为                                             ……… 8分

    （Ⅲ）                                   ………10分

    设

    △     

    ∴当时，函数的无极值点

    当时，函数有两个极值点                 ………12分

     

     


    同步练习册答案