
题目列表(包括答案和解析)
 如图所示,间距为L的光滑平行金属导轨,水平地放置在竖直方向的磁感应强度为B的匀强磁场中,一端接阻值是R的电阻.一电阻是R0,质量为m的导体棒放置在导轨上,在外力F作用下从t=0的时刻开始运动,不计导轨电阻,
如图所示,间距为L的光滑平行金属导轨,水平地放置在竖直方向的磁感应强度为B的匀强磁场中,一端接阻值是R的电阻.一电阻是R0,质量为m的导体棒放置在导轨上,在外力F作用下从t=0的时刻开始运动,不计导轨电阻,| π | 2ω |
 如图所示,间距为L的光滑平行金属导轨弯成“∠”型,底部导轨面水平,倾斜部分与水平面成θ角,导轨与固定电阻R相连,整个装置处于竖直向上的大小为B的匀强磁场中.有两导体棒ab和cd,质量均为m,两导体棒的电阻与固定电阻R阻值相等(阻值未知),垂直于导轨放置,且与导轨间接触良好,当导体棒cd沿底部导轨向右滑动速度为v时,导体棒ab恰好在倾斜导轨上处于静止状态,则此时( )
如图所示,间距为L的光滑平行金属导轨弯成“∠”型,底部导轨面水平,倾斜部分与水平面成θ角,导轨与固定电阻R相连,整个装置处于竖直向上的大小为B的匀强磁场中.有两导体棒ab和cd,质量均为m,两导体棒的电阻与固定电阻R阻值相等(阻值未知),垂直于导轨放置,且与导轨间接触良好,当导体棒cd沿底部导轨向右滑动速度为v时,导体棒ab恰好在倾斜导轨上处于静止状态,则此时( )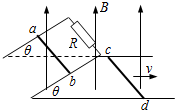 如图所示,间距为L的光滑平行金属导轨弯成“∠”型,底部导轨面水平,倾斜部分与水平面成θ角,导轨与固定电阻R相连,整个装置处于竖直向上的大小为B的匀强磁场中.导体棒ab和cd,质量均为m,垂直于导轨放置,且与导轨间接触良好,两导体棒的电阻与固定电阻R阻值相等,其余部分电阻不计,当导体棒cd沿底部导轨向右以速度为v匀速滑动时,导体棒ab恰好在倾斜导轨上处于静止状态,则导体棒ab消耗的热功率与cd棒克服安培力做功的功率之比为
如图所示,间距为L的光滑平行金属导轨弯成“∠”型,底部导轨面水平,倾斜部分与水平面成θ角,导轨与固定电阻R相连,整个装置处于竖直向上的大小为B的匀强磁场中.导体棒ab和cd,质量均为m,垂直于导轨放置,且与导轨间接触良好,两导体棒的电阻与固定电阻R阻值相等,其余部分电阻不计,当导体棒cd沿底部导轨向右以速度为v匀速滑动时,导体棒ab恰好在倾斜导轨上处于静止状态,则导体棒ab消耗的热功率与cd棒克服安培力做功的功率之比为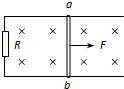 如图所示,间距为L的光滑平行金属导轨水平放置,匀强磁场的磁感应强度为B,方向垂直于导轨平面向下.导轨上有一质量为m、长为L的金属棒ab,金属棒电阻为R,导轨的一端连接阻值也为R的电阻,导轨电阻不计,金属棒ab在一水平恒力F作用下由静止开始向右运动,棒与导轨始终保持良好接触.求:
如图所示,间距为L的光滑平行金属导轨水平放置,匀强磁场的磁感应强度为B,方向垂直于导轨平面向下.导轨上有一质量为m、长为L的金属棒ab,金属棒电阻为R,导轨的一端连接阻值也为R的电阻,导轨电阻不计,金属棒ab在一水平恒力F作用下由静止开始向右运动,棒与导轨始终保持良好接触.求:如图所示,间距为L的光滑平行金属导轨水平放置,导轨上有一电阻为r的金属棒ab与导轨接触良好。导轨一端连接电阻R,其它电阻不计,磁感应强度为B,金属棒ab在水平外力F的作用下以速度v向右作匀速运动,则
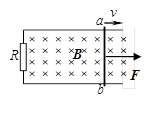
A.金属棒a端电势比b端高
B.电阻R两端的电压为BLv
C.ab棒受到的安培力的方向向左
D.外力F做的功等于电阻R上发出的焦耳热
一、单项选择题:(每小题4分,共24分)
1
2
3
4
5
6
C
C
D
C
7
8
9
10
11
BCD
BD
BCD
二、不定项选择题(每小题5分,共25分)
三、填空题(每小题5分,共40分;第一空2分,第二空3分)
12、,
13、10,288.7
14、,h┱(Ssinθ-h cosθ)
15、v=(2+4n)m/s(n=0,1,2,……)[写(2+8n)或(6+8n)也正确],负
16、,
17、2,直线截距下移、斜率减小
18、1┱6,
19、2,>
四、计算题:
20、(10分)
(1)从活塞上方的压强达到p0到活塞上方抽成真空的过程为等温过程:
1.5p0´V1=0.5p0´V2(2分),V2=3V1(1分),
缓慢加热,当活塞刚碰到玻璃管顶部时为等压过程:
=(2分),T2=1.2 T1,(1分)
(2)继续加热到1.8T1时为等容过程:
=(公式2分,代入1分),p=0.75p0(1分)
21、(10分)
不正确。(1分)由于小球沿圆弧CEA运动不是匀变速运动,不能仅根据末速度大小和路程来比较t1与t2的大小。(1分)
正确解:设CDA斜面倾角为θ
则 2R sin q=at12=gt12 sin q(R为圆半径)(2分)
解得t1==s=0.89s (1分)
物体沿圆弧CEA运动时,由于圆弧CEA对应的圆心角小于5°,所以小球的运动可以看成单摆的简谐振动,所以有t2===0.7s (3分)
所以 t1>t2。(2分)
22、(12分)
(1)电动机的功率 P=UI=1200W (2分)
电动机输出的机械功率 P机=ηP电=720W (1分)
当汽车以最大速度行驶时 F牵=Ff=0.05Mg=300N (1分)
根据 P机=F牵vm (2分)
求出最大速度 vm=2.4(m/s) (1分)
(2)设太阳到地面的距离是R,以太阳为球心,以R为半径的面积为S=4πR2
由题意可知=P0 得:R= (3分)
代入数据求出 R=1.5×
23.(13分)
(1)小轮对斜面的压力FN=Mg/cosθ(2分)
对斜面体进行受力分析,可知F=FN sinθ=Mgsinθ/cosθ(3分)=750N(2分)
(2)根据运动的分解:vM=vm tanθ (2分)
根据系统机械能守恒:Mgh=M vM2+m vm2 (3分)
两式联立,解得斜面体的速度: vm=≈
24.(14分)
(1)由表格中数据可知:金属棒先做加速度减小的加速运动,最后以
PG=mgv=0.01×10×7=0.7W (公式1分,结果1分)
(2)根据动能定理:WG+W安=mvt2-mv02 (2分)
W安=mvt2-mv02-mgh=×0.01×72-0.01×10×3.5=-0.105J(1分)
QR=E电=×0.105=0.06 J (2分)
(3)当金属棒匀速下落时,G=F安 → mg=BIL= (2分)
解得:BL==0.1 (1分)
电量q=It===
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com