
题目列表(包括答案和解析)
(本小题满分14分)
设![]() 为抛物线
为抛物线![]() 上的两个动点,过
上的两个动点,过![]() 分别作抛物线
分别作抛物线![]() 的切线
的切线![]() ,与
,与![]() 分别交于
分别交于![]() 两点,且
两点,且![]() ,若
,若![]()
若![]() ,求点
,求点![]() 的轨迹方程
的轨迹方程
(2)当![]() 所在直线满足什么条件时,P的轨迹为一条直线?(请千万不要证明你的结论)
所在直线满足什么条件时,P的轨迹为一条直线?(请千万不要证明你的结论)
(3)在满足(1)的条件下,求证:![]() 的面积为一个定值,并求出这个定值
的面积为一个定值,并求出这个定值
(本小题满分14分)已知![]() 抛物线
抛物线![]()
(1)设![]() 是C1的任意两条互相垂直的切线,并设
是C1的任意两条互相垂直的切线,并设![]() ,证明
,证明![]() :点M的纵坐标为定值;
:点M的纵坐标为定值;![]()
(2)在C1上是否存在点P,使得C1在点P处切线与C2相交于两点A、B,且AB的中垂线恰为C1的切线?若存在,求出点P的坐标;若不存在,说明理由。
(本小题满分14分)已知抛物线![]() ,椭圆经过点
,椭圆经过点![]() ,它们在
,它们在![]() 轴上有共同焦点,椭圆的对称轴是坐标轴.(Ⅰ)求椭圆的方程;(Ⅱ)若
轴上有共同焦点,椭圆的对称轴是坐标轴.(Ⅰ)求椭圆的方程;(Ⅱ)若![]() 是椭圆上的点,设
是椭圆上的点,设![]() 的坐标为
的坐标为![]() (
(![]() 是已知正实数),求
是已知正实数),求![]() 与
与![]() 之间的最短距离.
之间的最短距离.
(本小题满分14分)
已知抛物线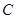 的顶点为坐标原点,焦点在
的顶点为坐标原点,焦点在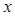 轴上. 且经过点
轴上. 且经过点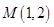 ,
,
(1)求抛物线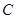 的方程;
的方程;
(2)若动直线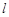 过点
过点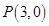 ,交抛物线
,交抛物线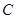 于
于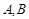 两点,是否存在垂直于
两点,是否存在垂直于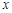 轴的直线
轴的直线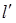 被以
被以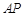 为直径的圆截得的弦长为定值?若存在,求出
为直径的圆截得的弦长为定值?若存在,求出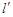 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(本小题满分14分)已知抛物线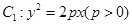 的焦点
的焦点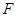 以及椭圆
以及椭圆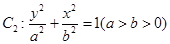 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆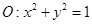 上.
上.
(Ⅰ)求抛物线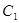 和椭圆
和椭圆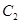 的标准方程;
的标准方程;
(Ⅱ)过点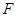 的直线交抛物线
的直线交抛物线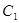 于
于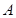 、
、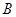 两不同点,交
两不同点,交 轴于点
轴于点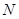 ,已知
,已知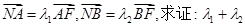 为定值.
为定值.
(Ⅲ)直线 交椭圆
交椭圆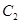 于
于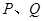 两不同点,
两不同点,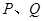 在
在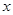 轴的射影分别为
轴的射影分别为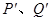 ,
, ,若点
,若点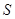 满足:
满足: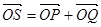 ,证明:点
,证明:点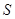 在椭圆
在椭圆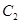 上.
上.
一、 选择题(本大题共12小题,每小题5分,共60分)
CDAB CDAB ABBA
二、填空题:(本大题共4小题,每小题4分,共16分)
13、 14、
14、
15、 16、
16、
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤。
17、解、由题 得
得 ,则
,则

0



2


0


递增
极大值
递减
当 时,
时, ;当
;当 时,
时, ;当
;当 时,
时,
所以,当 时,
时, ;当
;当 时,
时,
18、解、(1)设甲投球一次命中为事件A, ;设乙投球一次命中为事件B,
;设乙投球一次命中为事件B,
则甲、乙两人在罚球线各投球一次,恰好命中一次的概率

答:甲、乙两人在罚球线各投球一次,恰好命中一次的概率为 。
。
(2)甲、乙两人在罚球线各投球二次,这四次投球中至少一次命中的对立面是这四次投球中无一次命中,
所以甲、乙两人在罚球线各投球二次,这四次投球中至少一次命中的的概率是

答:甲、乙两人在罚球线各投球二次,这四次投球中至少一次命中的的概率是 。
。
19、解、(1) 中,
中,


(2)以 分别为
分别为 轴,如图建立直角坐标系,设
轴,如图建立直角坐标系,设
则


所以 与平面
与平面 所成的角为
所成的角为 。
。
20、解:(1)∵
依题意得 ∴
∴

(2)设第r +1项含x3项,
则

∴第二项为含x3的项:T2=-2 =-18x3
=-18x3
21、解、(1)设 ,若
,若
得 ,又
,又 ,所以
,所以
 得
得 ,而
,而 ,所以无解。即直线
,所以无解。即直线 与直线
与直线 不可能垂直。
不可能垂直。
(2)

所以 的范围是
的范围是 。
。
22、(Ⅰ)解:当 时,
时, ,得
,得 ,且
,且
 ,
, .
.
所以,曲线 在点
在点 处的切线方程是
处的切线方程是 ,整理得
,整理得
 .。
.。
(Ⅱ)解:
 .
.
令 ,解得
,解得 或
或 .
.
由于 ,以下分两种情况讨论.
,以下分两种情况讨论.
(1)若 ,当
,当 变化时,
变化时, 的正负如下表:
的正负如下表:












因此,函数 在
在 处取得极小值
处取得极小值 ,且
,且
 ;
;
函数 在
在 处取得极大值
处取得极大值 ,且
,且
 .
.
(2)若 ,当
,当 变化时,
变化时, 的正负如下表:
的正负如下表:












因此,函数 在
在 处取得极小值
处取得极小值 ,且
,且
 ;
;
函数 在
在 处取得极大值
处取得极大值 ,且
,且
 .
.
(Ⅲ)证明:由 ,得
,得 ,当
,当 时,
时,
 ,
, .
.
由(Ⅱ)知, 在
在 上是减函数,要使
上是减函数,要使 ,
,
只要
即
 ①
①
设 ,则函数
,则函数 在
在 上的最大值为
上的最大值为 .
.
要使①式恒成立,必须 ,即
,即 或
或 .
.
所以,在区间 上存在
上存在 ,使得
,使得 对任意的
对任意的 恒成立.
恒成立.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com