（本小题满分12分．其中（Ⅰ）小问6分，（Ⅱ）小问6分）

已知，数列{a_n}满足：,．

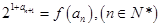（Ⅰ）求证：；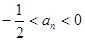

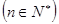（Ⅱ）判断a_n与a_n+1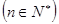的大小，并说明理由．

（本小题满分12分．其中（Ⅰ）小问6分，（Ⅱ）小问6分）

如图，已知四棱锥P-ABCD的底面ABCD是边长为2的正方形，PD⊥底面ABCD，E、F分别为棱BC、AD的中点．

（Ⅰ）若PD=1，求异面直线PB和DE所成角的余弦值；

（Ⅱ）若二面角P-BF-C的余弦值为，求四棱锥P-ABCD的体积

（本小题满分12分）

道路交通安全法中将饮酒后违法驾驶机动车的行为分成两个档次：“酒后驾车”和“醉酒驾车”，其检测标准是驾驶人员血液中的酒精含量Q（简称血酒含量，单位是毫克/100毫升），当20≤Q<80时，为酒后驾车；当Q≥80时，为醉酒驾车．某市公安局交通管理部门在某路段的一次拦查行动中，依法检查了200辆机动车驾驶员的血酒含量，其中查处酒后驾车的有6人，查处醉酒驾车的有2人，依据上述材料回答下列问题：

   （Ⅰ）分别写出违法驾车发生的频率和醉酒驾车占违法驾车总数的百分数；

（Ⅱ）从违法驾车的8人中抽取2人，求取到醉酒驾车人数的分布列和期望。

（Ⅲ）饮酒后违法驾驶机动车极易发生交通事故，假设酒后驾车和醉酒驾车发生交通事故的概率分别是0．1和0．25，且每位驾驶员是否发生交通事故是相互独立的。依此计算被查处的8名驾驶员中至少有一人发生交通事故的概率（列式）。

（本小题满分12分）

有编号为,,…的10个零件，测量其直径（单位：cm），得到下面数据：

其中直径在区间[1.48，1.52]内的零件为一等品。

（Ⅰ）从上述10个零件中，随机抽取一个，求这个零件为一等品的概率；

（Ⅱ）从一等品零件中，随机抽取2个.

     （ⅰ）用零件的编号列出所有可能的抽取结果；

     （ⅱ）求这2个零件直径相等的概率。本小题主要考查用列举法计算随机事件所含的基本事件数及事件发生的概率等基础知识，考查数据处理能力及运用概率知识解决简单的实际问题的能力。满分12分

【解析】（Ⅰ）解：由所给数据可知，一等品零件共有6个.设“从10个零件中，随机抽取一个为一等品”为事件A，则P（A）==.

      （Ⅱ）（i）解：一等品零件的编号为.从这6个一等品零件中随机抽取2个，所有可能的结果有：,,,

,,,共有15种.

      (ii)解：“从一等品零件中，随机抽取的2个零件直径相等”（记为事件B）的所有可能结果有：，，共有6种.

      所以P(B)=.

（本小题满分12分）

如图，在五面体ABCDEF中，四边形ADEF是正方形，FA⊥平面ABCD，BC∥AD，CD=1，AD=，∠BAD＝∠CDA＝45°.

（Ⅰ）求异面直线CE与AF所成角的余弦值；      

（Ⅱ）证明CD⊥平面ABF；

（本小题满分12分）

有编号为,,…的10个零件，测量其直径（单位：cm），得到下面数据：

其中直径在区间[1.48，1.52]内的零件为一等品。

（Ⅰ）从上述10个零件中，随机抽取一个，求这个零件为一等品的概率；

（Ⅱ）从一等品零件中，随机抽取2个.

     （ⅰ）用零件的编号列出所有可能的抽取结果；

     （ⅱ）求这2个零件直径相等的概率。本小题主要考查用列举法计算随机事件所含的基本事件数及事件发生的概率等基础知识，考查数据处理能力及运用概率知识解决简单的实际问题的能力。满分12分

【解析】（Ⅰ）解：由所给数据可知，一等品零件共有6个.设“从10个零件中，随机抽取一个为一等品”为事件A，则P（A）==.

      （Ⅱ）（i）解：一等品零件的编号为.从这6个一等品零件中随机抽取2个，所有可能的结果有：,,,

,,,共有15种.

      (ii)解：“从一等品零件中，随机抽取的2个零件直径相等”（记为事件B）的所有可能结果有：，，共有6种.

      所以P(B)=.

（本小题满分12分）

如图，在五面体ABCDEF中，四边形ADEF是正方形，FA⊥平面ABCD，BC∥AD，CD=1，AD=，∠BAD＝∠CDA＝45°.

（Ⅰ）求异面直线CE与AF所成角的余弦值；      

（Ⅱ）证明CD⊥平面ABF；